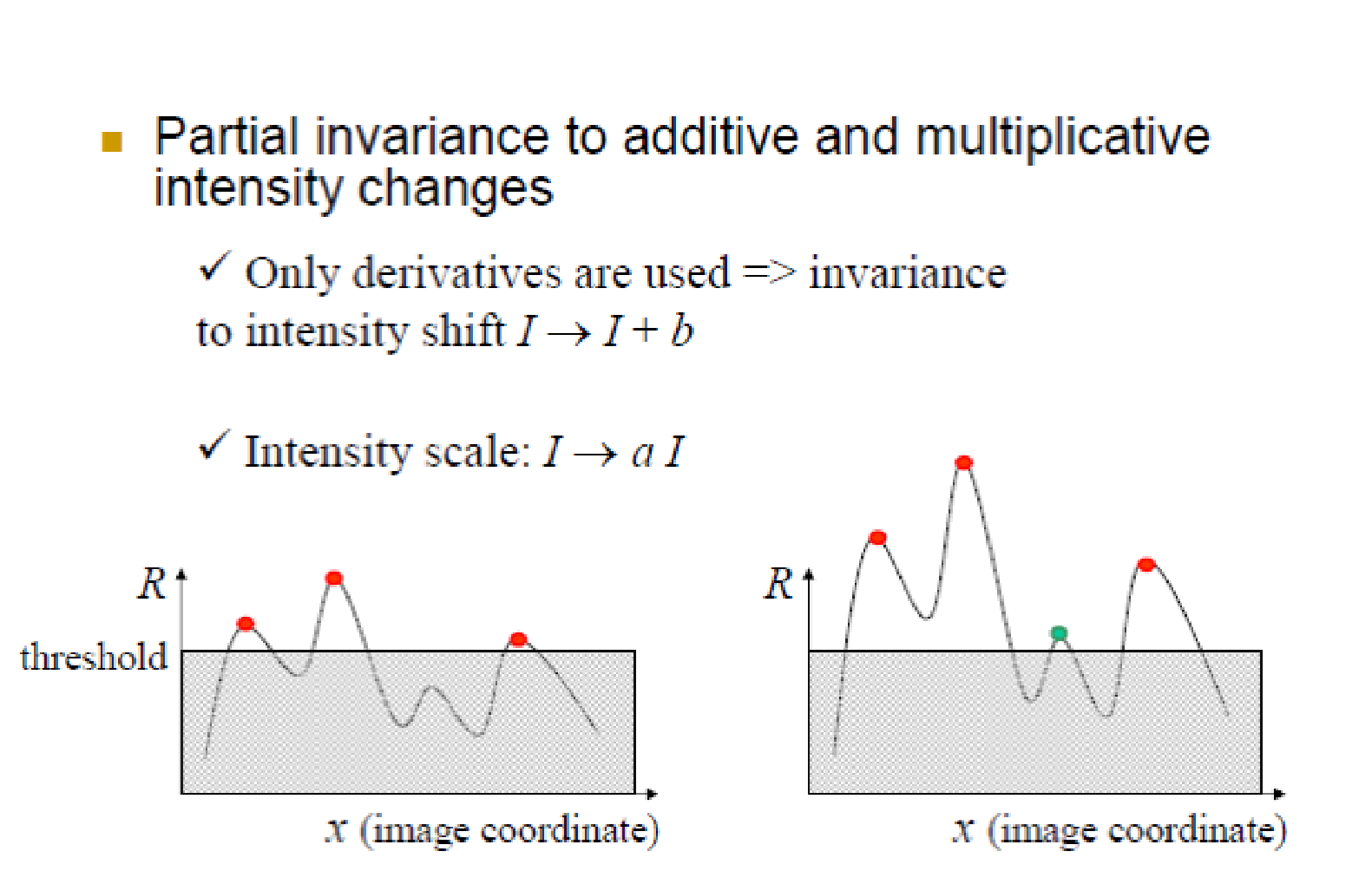
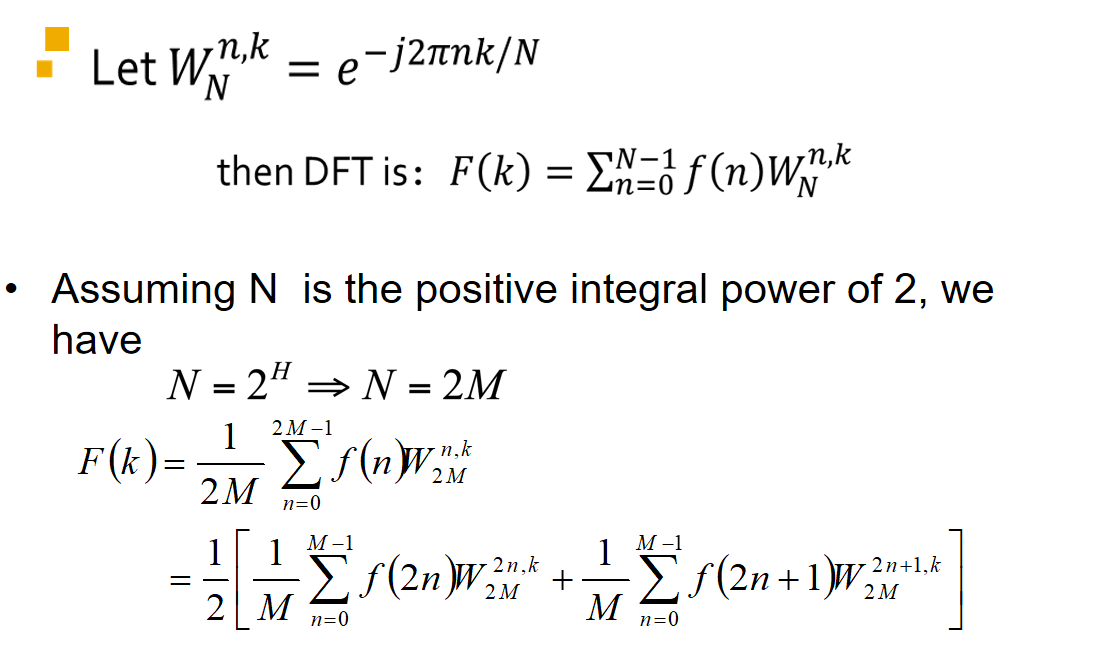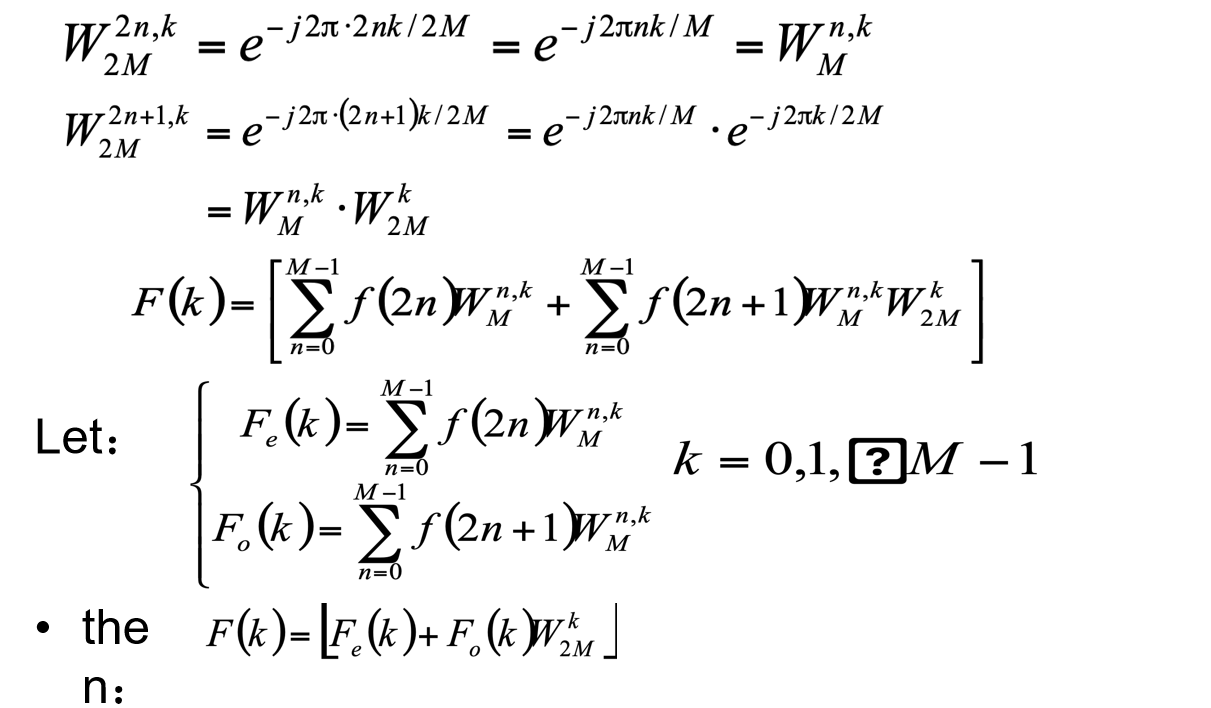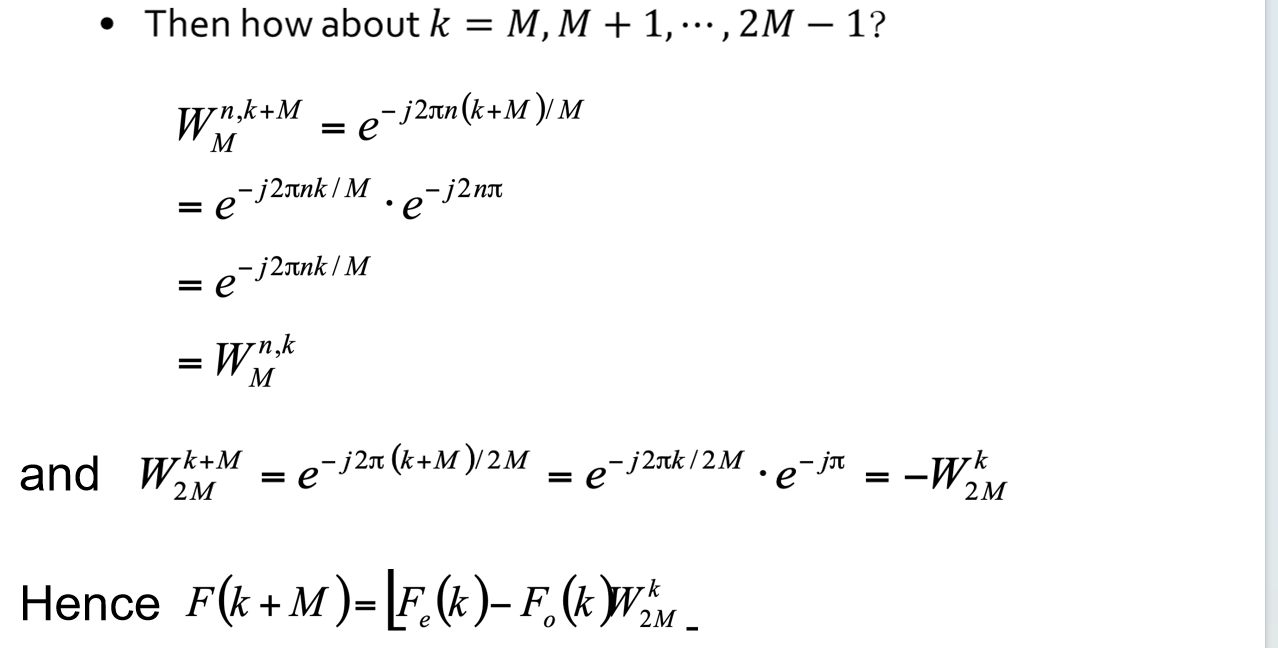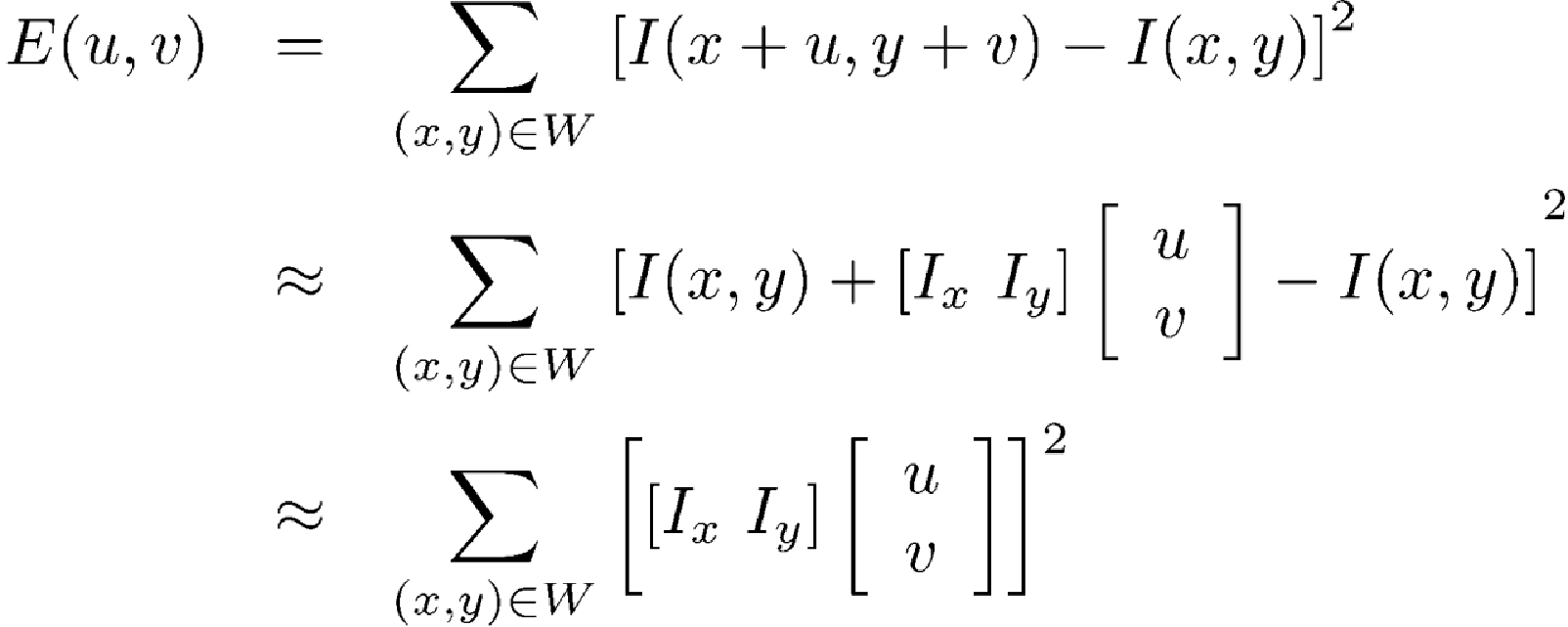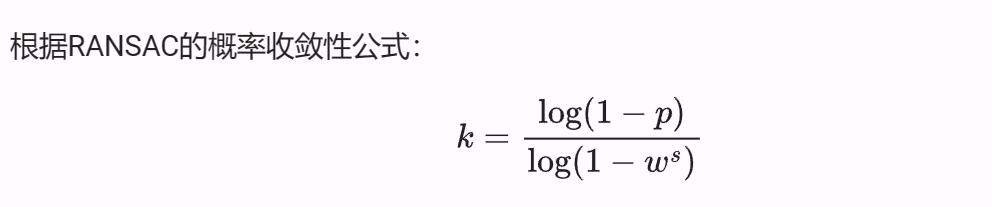跳转至

Introduction

  1. 不同形式的成像

image-20240106092529162

Ch1

约 8764 个字 23 行代码 87 张图片 预计阅读时间 44 分钟

* 成像过程

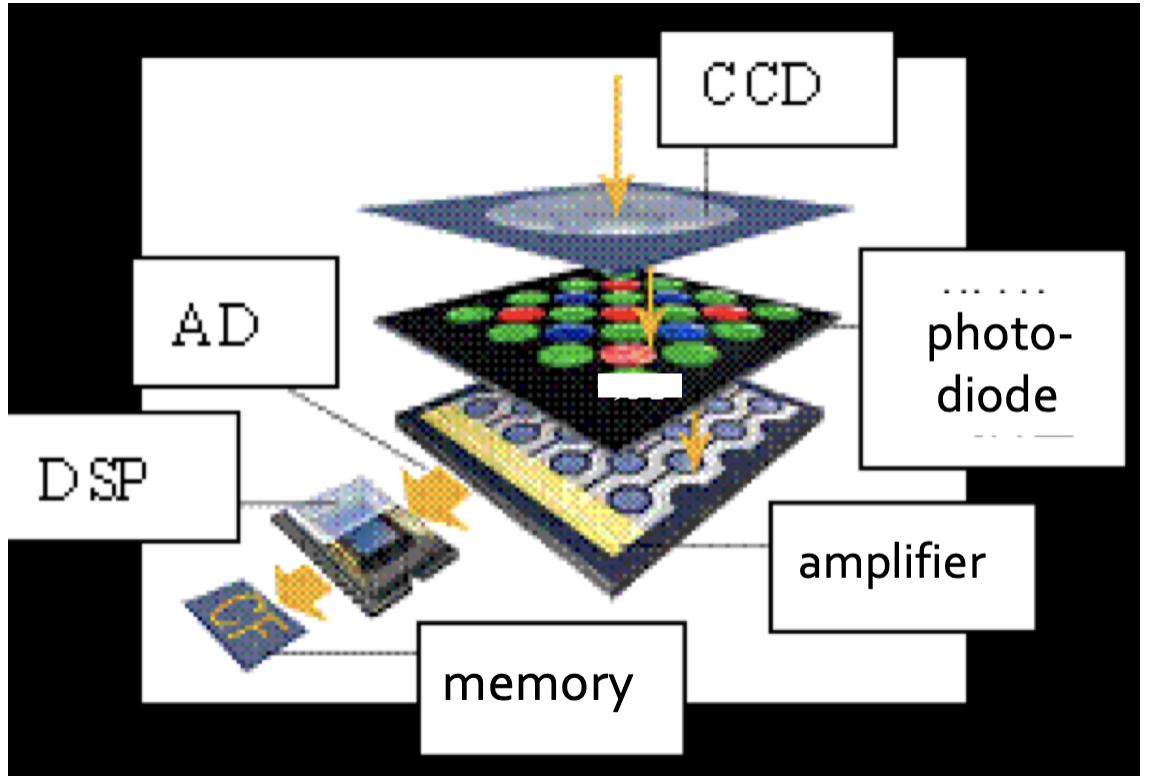
image-20240106094910555

(1)当使用数码相机拍摄景物时，景物反射的光线通过数码相机的镜头透射到CCD上。
(2)当CCD曝光后，光电二极管受到光线的激发而释放出电荷，生成感光元件的电信号。
(3) CCD控制芯片利用感光元件中的控制信号线路对发光二极管产生的电流进行控制，由电流传输电路输出，CCD会将一次成像产生的电信号收集起来，统一输出到放大器。
(4)经过 放大和滤波后 的电信号被传送到ADC，由ADC将电信号（模拟信号）转换为数字信号，数值的大小和电信号的强度与电压的高低成正比，这些数值其实也就是图像的数据。
(5)此时这些图像数据还不能直接生成图像，还要输出到DSP（数字信号处理器）中，在DSP中，将会对这些图像数据进行色彩校正、白平衡处理，并编码为数码相机所支持的图像格式、分辨率，然后才会被存储为图像文件。
(6)当完成上述步骤后，图像文件就会被保存到存储器上,我们就可以欣赏了。

光圈对于成像的影响

光圈孔径⼤的时候，会导致模糊；

光圈孔径过⼩的时候，可通过的光线就很少，导致光强太弱，同时当孔径⼩到⼀定程度时，会产⽣衍射现象。

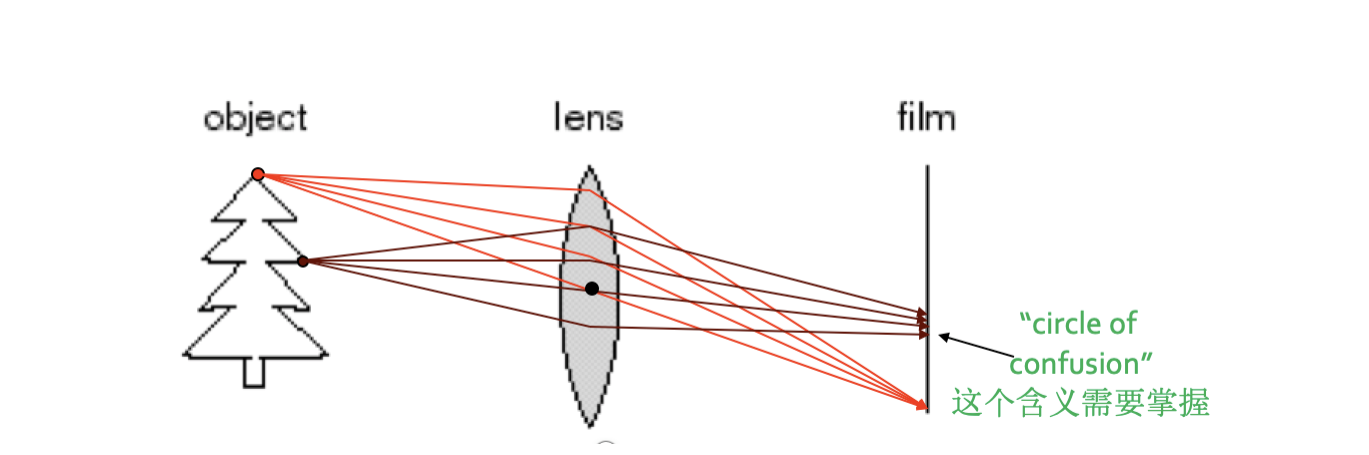
弥散圆的定义

image-20240106094938816

通过使⽤透镜可以会聚更多的光线到⼀个成像点，只是只有在特殊的位置上才能达到这个⽬标，位于合适距离的物体点可以成清晰像，其他的点则会产⽣弥散圆。弥散圆是指在焦点前后，光线开始聚集和扩散，点的影像变模糊，形成⼀个扩⼤的圆。

如果弥散圆的直径⼩于⼈眼的鉴别能⼒，在⼀定范围内实际影像产⽣的模糊是不能辨认的。不能辨认的直径叫做容许弥散圆。

**光圈对于景深的影响

焦点前后各有⼀个容许弥散圆，他们之间的距离叫做景深。景深随镜头的焦距、光圈值、拍摄距离⽽变化

(1)、镜头光圈 光圈越⼤，景深越⼩；光圈越⼩，景深越⼤； (2)、镜头焦距 镜头焦距越⻓，景深越⼩；焦距越短，景深越⼤； (3)、拍摄距离 距离越远，景深越⼤；距离越近，景深越⼩

彩⾊和消⾊的定义

彩⾊是指红、⻩、蓝等单⾊以及它们的混合⾊。彩⾊物体对光谱各波⻓的反射具有选择性，所以它们在⽩光照射下呈现出不同的颜⾊。

消⾊，也就是灰度，是指⽩⾊，⿊⾊以及各种深浅不同的灰⾊。消⾊物体对光谱各波⻓的反射没有选择性，它们是中性⾊。

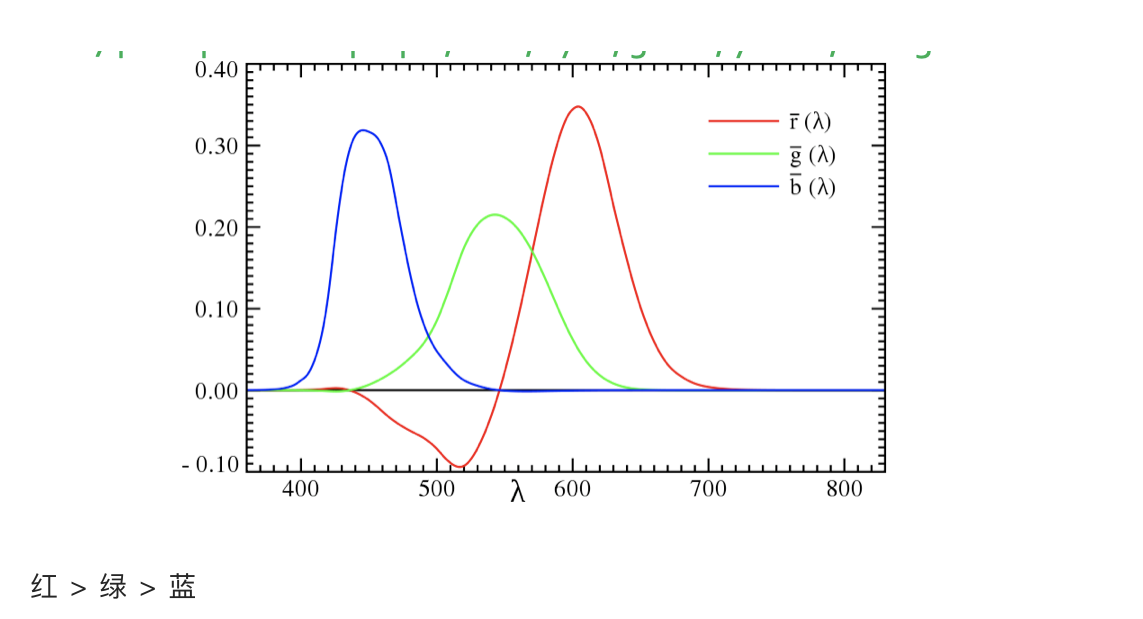
红绿蓝光的波⻓

image-20240106095009857

红 > 绿 > 蓝

视⽹膜的两种细胞

视⽹膜上分布着两种视觉细胞，⼀种为杆状体，另⼀种为锥状体。杆状体细胞⽐较多，⼤约有上亿个，它对光极为灵敏，但没有区分⾊彩的能⼒。锥状体细胞则只有六、七百万个，它要在较强的照度下才能激发，它的存在使我们能够辨别各种不同的颜⾊。

杆状：多，对光灵敏，但是不能区分⾊彩 锥状：少，强光才能激发，⽤来区分⾊彩

三原⾊形成的原理

在视⽹膜上存在着三种分别对红、绿和蓝光线的波⻓特别敏感的视锥细胞或相应的感光⾊素，当不同波⻓的光线进⼊⼈眼时，与之相符或相近的视锥细胞发⽣不同程度的兴奋，于是在⼤脑产⽣相应的⾊觉；三种视锥细胞若受到同等程度的刺激，则产⽣消⾊。

感知的优先程度和敏感度

优先程度：同等条件下，⼈们往往会注意到⾊调（Hue, H）的变化，然后是饱和度（Saturation, S），然后是亮度（Value, V）。调保亮 HSV

敏感度：⼈眼对于亮度的变化最为敏感，分辨能⼒最强。恰好与⼈眼的⾼动态能⼒相匹配。

* 与设备相关和⽆关的颜⾊模型

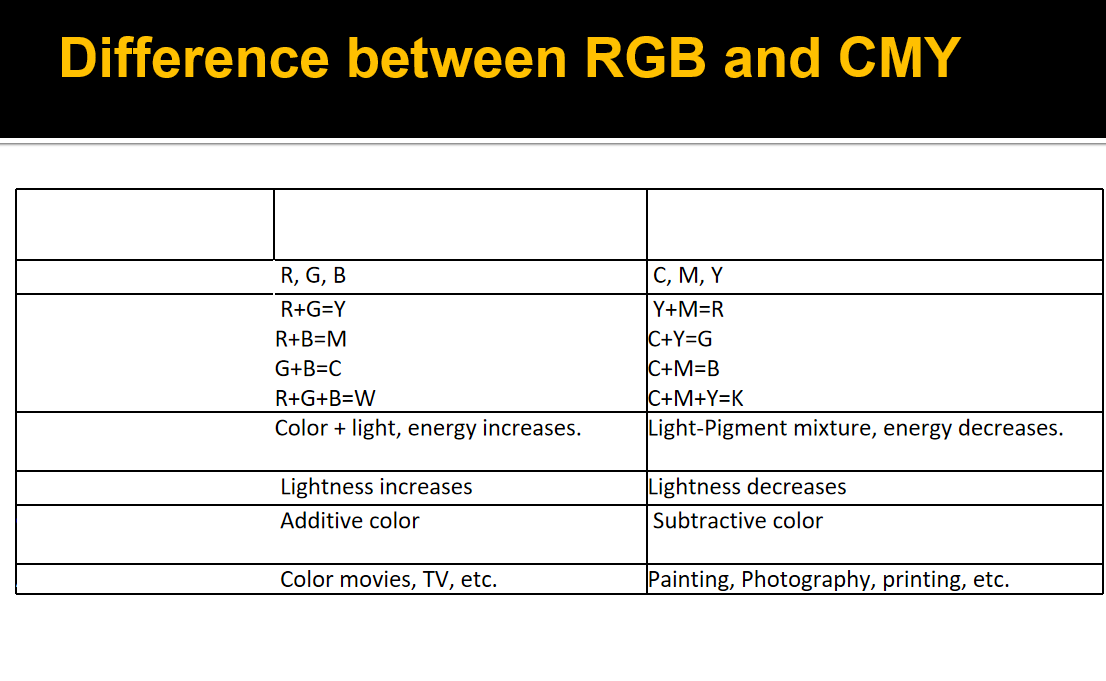
  1. 与设备相关的颜⾊模型：RGB, CMY, HSV

  2. 与设备⽆关的颜⾊模型：CIE XYZ, CIE L*a*b和 CIE YUV

HSV更接近⼈的感知

RGB

image-20240110150508124

RBG 颜色模型是三维直角坐标颜色系统中的一个单位正方体在正方体的主对角线上，各原色的量相等，产生由暗到亮的白色，即灰度。（0，0，0）为黑，（1，1，1）为白，正方体的其他6个角点分别为红、黄、绿、青、蓝和品红。RGB颜色模型构成的颜色空间是CIE原色空间的一个真子集。RGB颜色模型通常用于彩色阴极射线管和彩色光栅图形显示器（计算机和电视机采用）。

HSV

image-20240106100534156

HSV颜色空间是从人的视觉系统出发，用色调（Hue)、色饱和度（Saturation）和亮度（Intensity，或者Value）来圆锥的顶面对应于V=1，它包含RGB模型中的R=1，G=1，B=1三个面，故所代表的颜色较亮。色度H由绕V轴的旋转角给定。红色对应于角度0o，绿色对应于角度120o，蓝色对应于角度240o。描述颜色。在圆锥的顶点处，V=0，H和S无定义，代表黑色。

加色 减色(加色的补色)

RGB CMY 彩色印刷或者彩色打印的纸张不能发射光线，因而印刷机或打印机就只能使用一些能够吸收特定光波而反射其他光波的油墨或者颜色。油墨或颜料的3种基色是以红、绿、蓝三色的补色青（Cyan）、品红（Magenta）、黄（Yellow）为基色。用CMY模型产生的颜色称为相减色，是因为它减掉了为视觉系统识别颜色所需要的反射光

image-20240104144759494

JPEG的压缩的基本策略以及优点

压缩策略:根据压缩⽐要求，从⾼频到低频逐步削减信息

好处：

  • ⾼频信息占⽤存储空间⼤，减少⾼频信息更容易获得⾼压缩⽐；
  • 低频信息可以保留物体的基本轮廓和⾊彩分布，最⼤限度维持图像质量。
  • 适合⽤于互联⽹

图像格式

目的：存储图像信息 图像特点：以像素为单位、矩形区域、信息量⼤

有些⽂件格式与操作系统有关：windows、unix、mac 编码⽅式：⽆压缩（BMP）、⽆损压缩(PNG,GIF)、有损压缩(JPEG)

常⽤的图像⽂件格式：BMP、JPEG、TIFF、GIF、PNG……

BMP

Windows操作系统的标准文件格式之一，有时候也存为.dib文件大部分BMP文件是不压缩的形式但它本身还是支持图像压缩的，如rle格式（行程长度编码，runlength encoding）压缩格式等

img

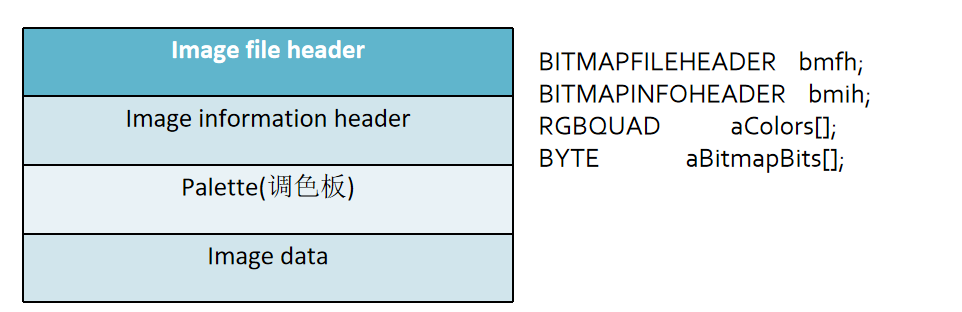
Image file header | 文件头

bfType说明文件的类型，该值必需是0x4D42，也就是字符'BM'。

bfSize说明该位图文件的大小，用字节为单位

bfReserved1保留，必须设置为0

bfReserved2保留，必须设置为0

bfOffBits说明从文件头开始到实际的图象数据之间的字节的偏移量。这个参数是非常有用的，因为位图信息头和调色板的长度会根据不同情况而变化，所以你可以用这个偏移值迅速的从文件中读取到位数据。

Image information header | 信息头

typedef struct tagBITMAPINFOHEADER{
// 长度固定  40
DWORD  biSize;
LONG            biWidth;
LONG            biHeight;
WORD           biPlanes;
WORD           biBitCount
DWORD  biCompression;
DWORD  biSizeImage;
LONG            biXPelsPerMeter;
LONG            biYPelsPerMeter;
DWORD  biClrUsed;
DWORD  biClrImportant;
} BITMAPINFOHEADER;

biSize How many bytes are needed to define 说明上述结构所需要的字数。

biWidth说明图象的宽度，以象素为单位。

biHeight说明图象的高度，以象素为单位。如果该值是一个正数，说明图像是倒向的，如果该值是一个负数，则说明图像是正向的。大多数的BMP文件都是倒向的位图，也就是时，高度值是一个正数。

biPlanes为目标设备说明位面数，其值将总是被设为1。

biBitCount说明比特数/象素，其值为1、4、8、16、24、或32。但是由于我们平时用到的图像绝大部分是24位和32位的，所以我们讨论这两类图像。

biCompression说明图象数据压缩的类型，我们只讨论没有压缩的类型：BI_RGB。

biSizeImage说明图象的大小，以字节为单位。当用BI_RGB格式时，可设置为0。

biSizeImage=biWidth’ × biHeight biWidth` 必须是 4 的倍数

biXPelsPerMeter说明水平分辨率，用象素/米表示。

biYPelsPerMeter说明垂直分辨率，用象素/米表示。

biClrUsed说明位图实际使用的彩色表中的颜色索引数（设为0的话，则说明使用所有调色板项）。

biClrImportant说明对图象显示有重要影响的颜色索引的数目，如果是0，表示都重要。

Palette | 调色板

| 含义 |

有一个长宽各为200个象素，颜色数为16色的彩色图，每一个象素都用R、G、B三个分量表示。因为每个分量有256个级别，要用8位(bit)，即一个字节(byte)来表示，所以每个象素需要用3个字节。整个图象要用200×200×3，约120k字节，可不是一个小数目呀！

如果我们用下面的方法，就能省的多。因为是一个16色图，也就是说这幅图中最多只有16种颜色，我们可以用一个表：表中的每一行记录一种颜色的R、G、B值。这样当我们表示一个象素的颜色时，只需要指出该颜色是在第几行，即该颜色在表中的索引值。举个例子，如果表的第0行为255，0，0(红色)，那么当某个象素为红色时，只需要标明0即可。这张R、G、B的表，就是我们常说的调色板(Palette)，另一种叫法是颜色查找表LUT(Look Up Table)，似乎更确切一些。Windows位图中便用到了调色板技术。其实不光是Windows位图，许多图象文件格式如pcx、tif、gif等都用到了。所以很好地掌握调色板的概念是十分有用的。

Palette N * 4 bytes. 每一个元素都有四个比特，分别存储蓝绿红的 RGB 值和一个 reserved byte.

Image data | 图像数据

image-20240106102013475

(1) 每一行的字节数必须是4的整倍数，如果不是，则需要补齐。这在前面介绍biSizeImage时已经提到了。

(2) 一般来说，.bMP文件的数据从下到上，从左到右的。也就是说，从文件中最先读到的是图象最下面一行的左边第一个象素，然后是左边第二个象素……接下来是倒数第二行左边第一个象素，左边第二个象素……依次类推 ，最后得到的是最上面一行的最右一个象素。

RLE 二值图像编码

  • 每一行都用subterm表示，第一个为行号，

image-20240104145020893

Ch2

⼆值图像的优缺点

优点：

  • 更⼩的内存需求
  • 运⾏速度更快
  • 为⼆值图像开发的算法往往可以⽤于灰度级图像
  • 更便宜

缺点：

  • 应⽤范围毕竟有限；
  • 更⽆法推⼴到三维空间中
  • 表现⼒⽋缺，不能表现物体内部细节
  • ⽆法控制对⽐度

图像的⼆值化

  1. 设置⼀个阈值

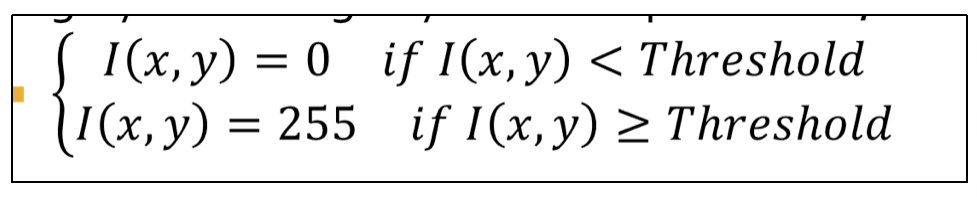
选取合适的阈值的基本思想

将⼆值化得到的⼆值图像视为两部分，⼀部分对应前景（Foreground），另⼀部分对应背景（Background）。尝试找到⼀个合适的threshold使得到的前景和背景的内部协⽅差最⼩，⽽它们之间的外部协⽅差最⼤。

⼤津算法

Step 1: 确定原始图像中像素的最⼤值和最⼩值；

Step 2: 最⼩值加1作为threshold对原始图像进⾏⼆值化操作；

Step 3: 根据对应关系确定前景和背景，分别计算当前threshold下的内部协⽅差和外部协⽅差；

Step 4: 回到Step 2直到达到像素最⼤值；

Step 5：找到最⼤外部和最⼩内部协⽅差对应的threshold.

局部⾃适应操作

设定⼀个局部窗⼝，在整个图像上滑动该窗⼝；对于每⼀窗⼝位置，确定针对该窗⼝的threshold。

膨胀(Dilation)

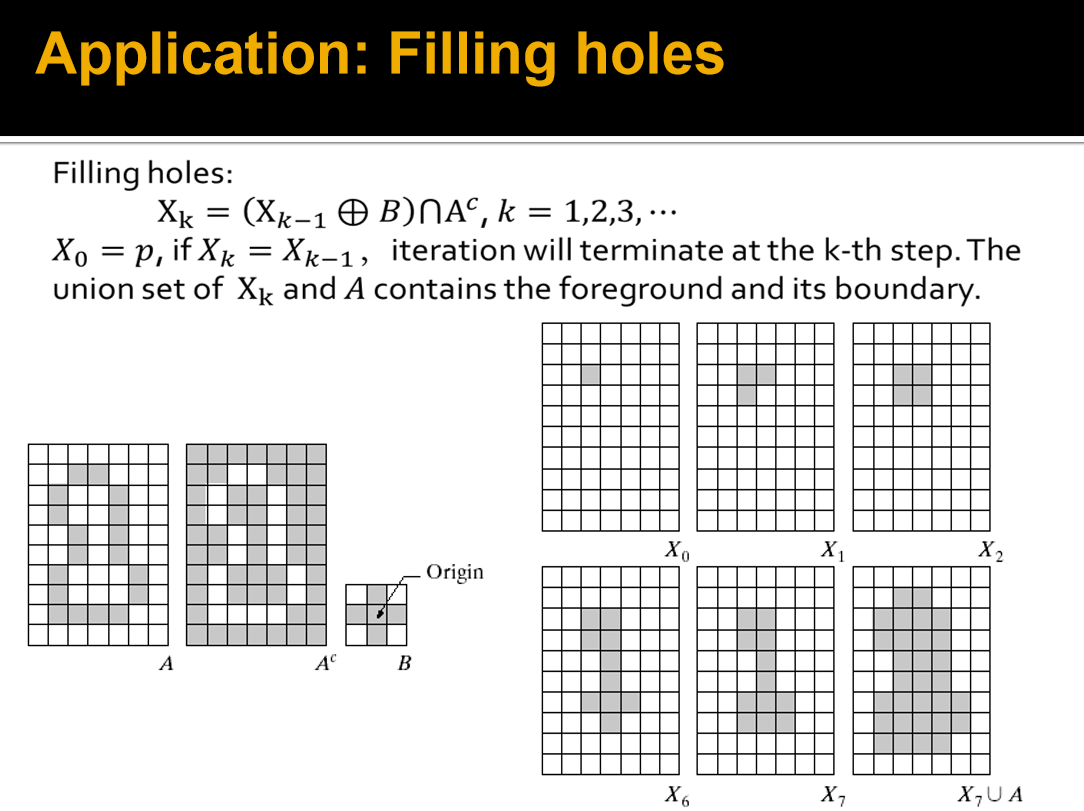
物理意义：使边界向外部扩张的过程，可以⽤来填补物体中的空洞。

image-20240106102221878

image-20240106102519957

腐蚀（Erosion）

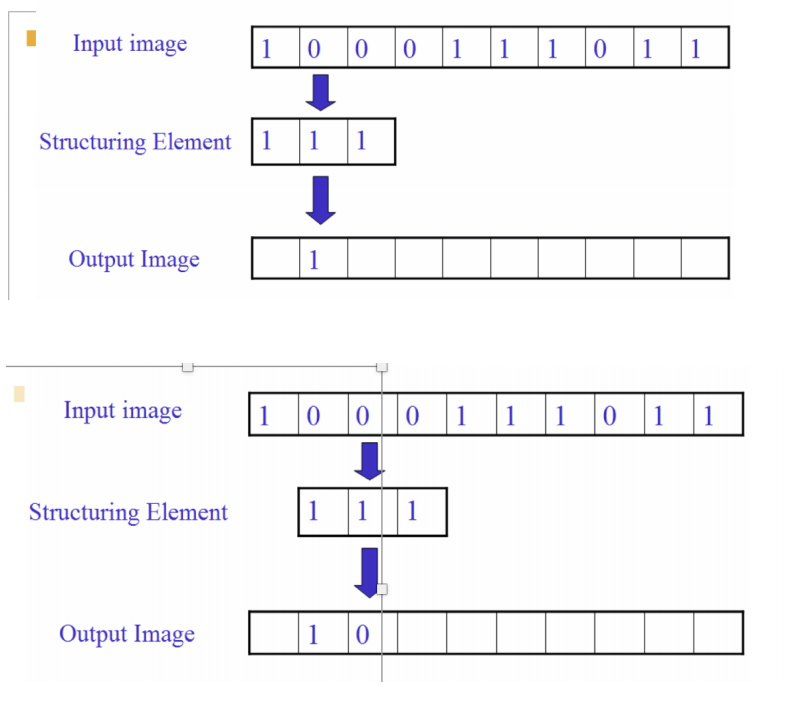
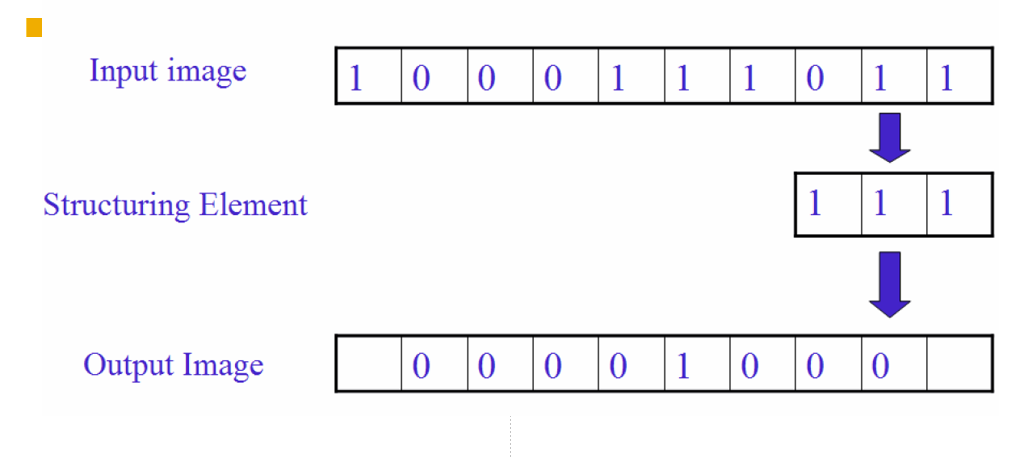
物理意义：消除边界点，使边界向内部收缩的过程。可以⽤来消除⼩且⽆意义的物体

image-20240106102551691

image-20240106102651308

Application

image-20240106103539464

*** 腐蚀和膨胀具有对偶性

image-20240104145434245

开运算(Opening = E + D)

先腐蚀，后膨胀。

物理意义：⽤来消除⼩物体、在纤细点处分离物体、平滑较⼤物体的边界的同时并不明显改变其积。

闭运算(Closing = D + E)

先膨胀后腐蚀

物理意义：⽤来填充物体内细⼩空洞、连接邻近物体、平滑其边界的同时并不明显改变其⾯积。

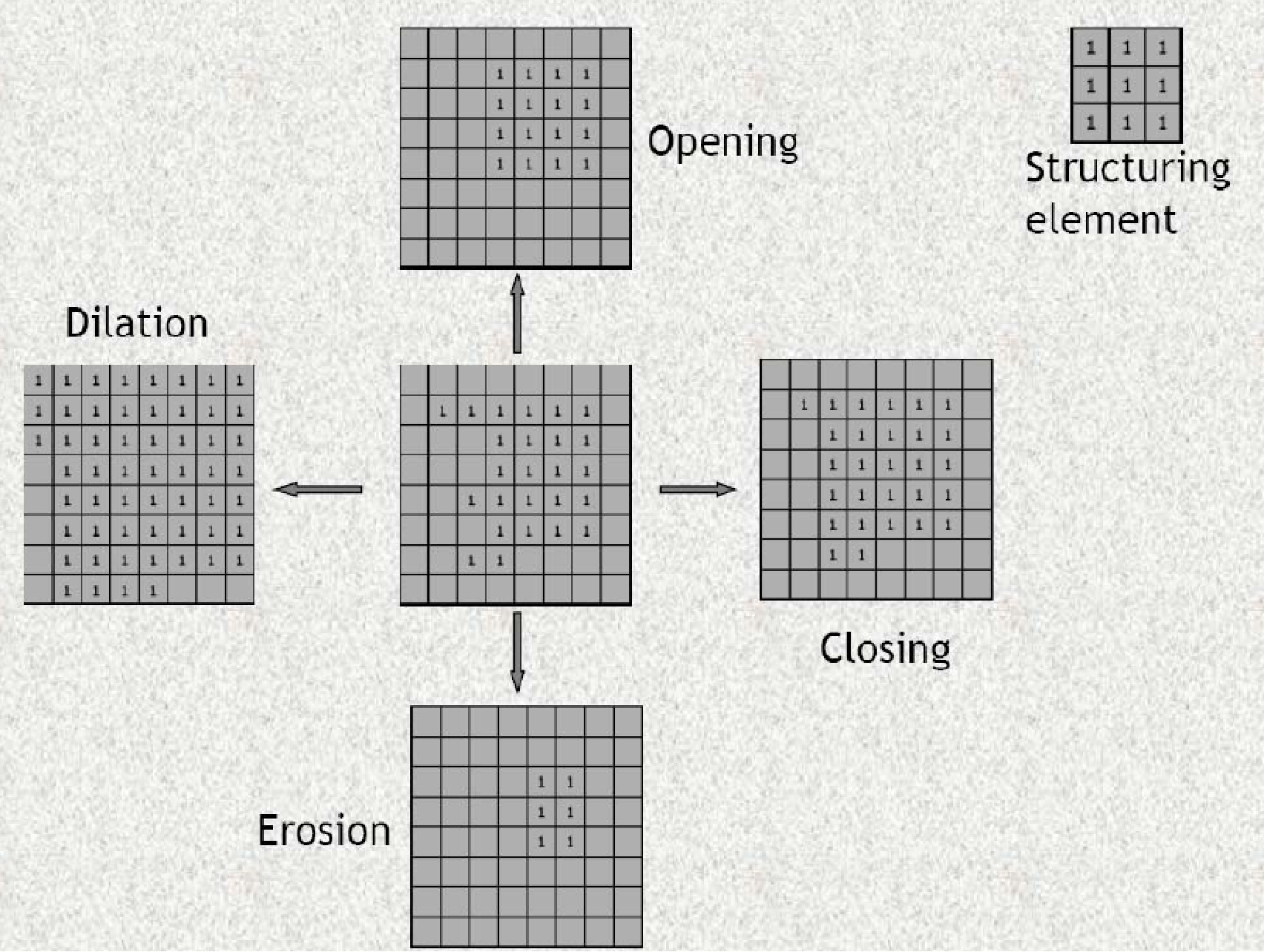
image-20240106103951459

指纹的预处理过程

  • Opening 消除外部噪点
  • 腐蚀
  • 膨胀
  • Closing 消除内部噪点

image-20240104145552006

Ch3

计算灰度感知

根据⻙伯定理

image-20240106104502041

** Log 可视化增强

Ld是显示亮度，Lw是真实亮度,Lmax是图像中的最⼤亮度。

这个映射能够确保不管场景的动态范围是怎么样的，其最⼤值都能映射到1（⽩），其他的值能够⽐较平滑地变化。

** 图像直方图均衡化

直方图均衡化实质上是减少图像的灰度级以换取对比度的加大。在均衡过程中，原来的直方图上出现概率较小的灰度级被归入很少几个甚至一个灰度级中，故得不到增强。若这些灰度级所构成的图象细节比较重要，则需采用局部区域直方图均衡化处理。

image-20240106104531917

假设：

  1. 令r和s分别代表变化前后图像的灰度级，并且 0≤r,s ≤1 。

  2. P(r)和P(s) 分别为变化前后各级灰度的概率密度函数（r和s值已归⼀化，最⼤灰度值为1）。

规定：

  1. 在0≤r ≤1中，T(r)是单调递增函数，并且0≤T(r)≤1。

  2. 反变换r = T-1(s)也为单调递增函数。

灰度直⽅图均衡化

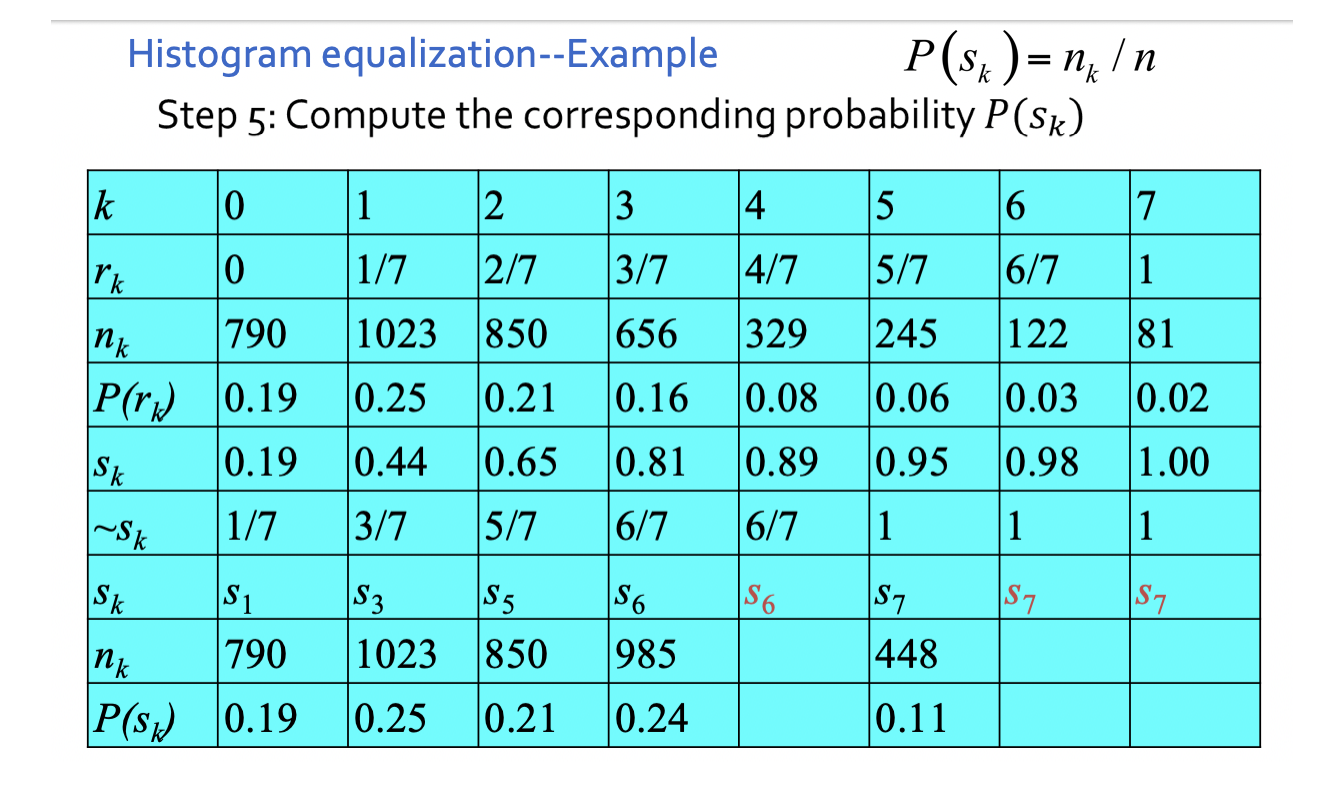
设图像有64*64=4096个像素，有8个灰度级，灰度分布：

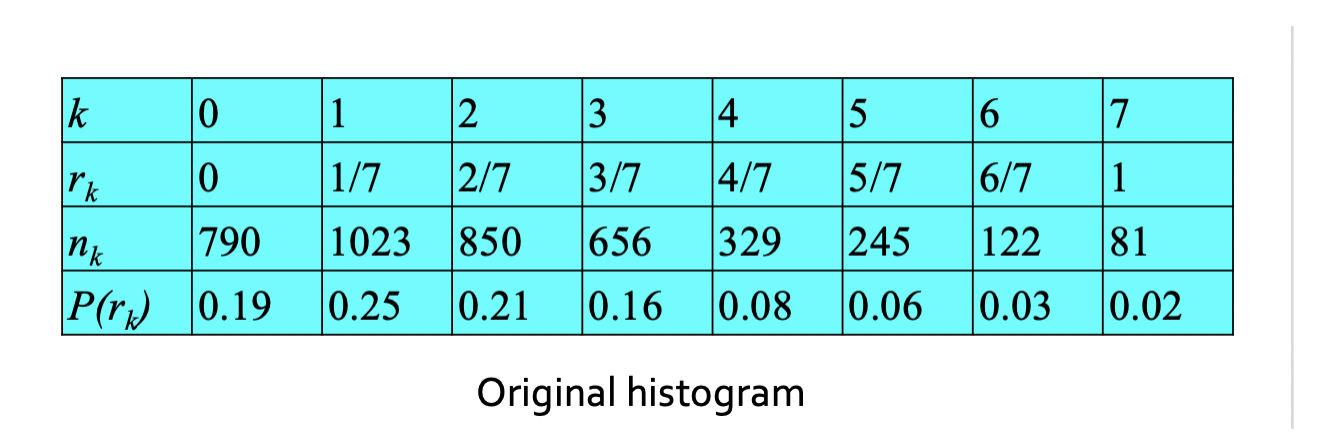
image-20240106104558484

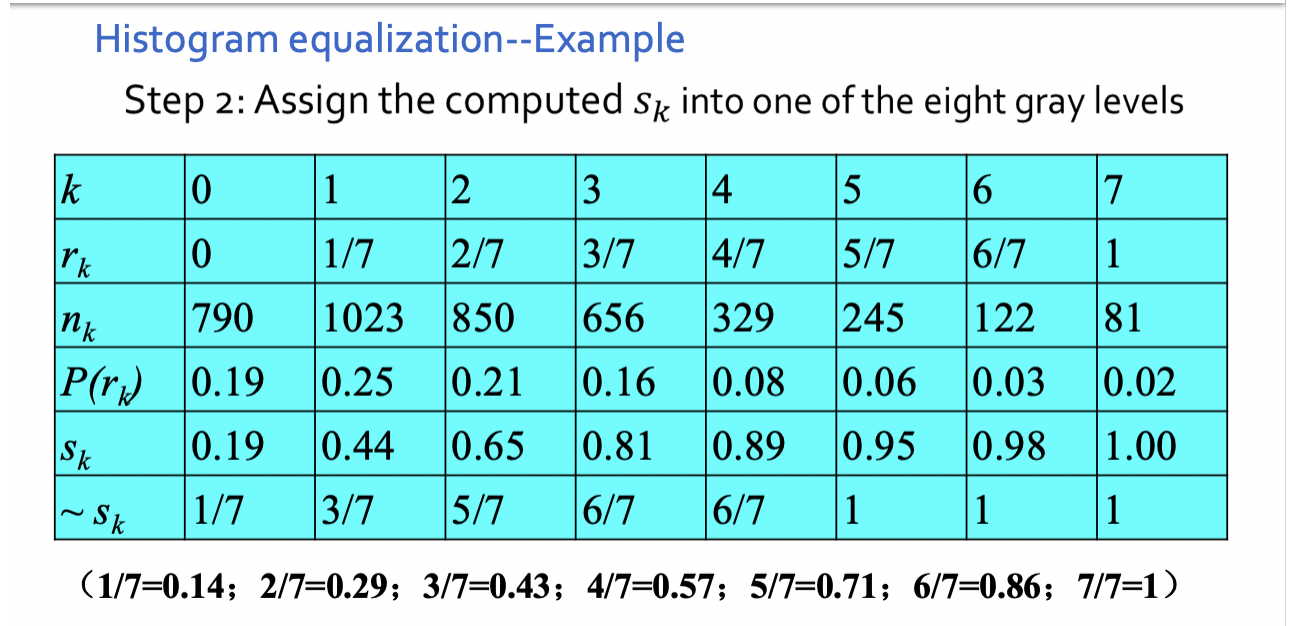
如果在1/7和2/7之间，那么和哪个更近就约算到哪个

image-20240106104606985

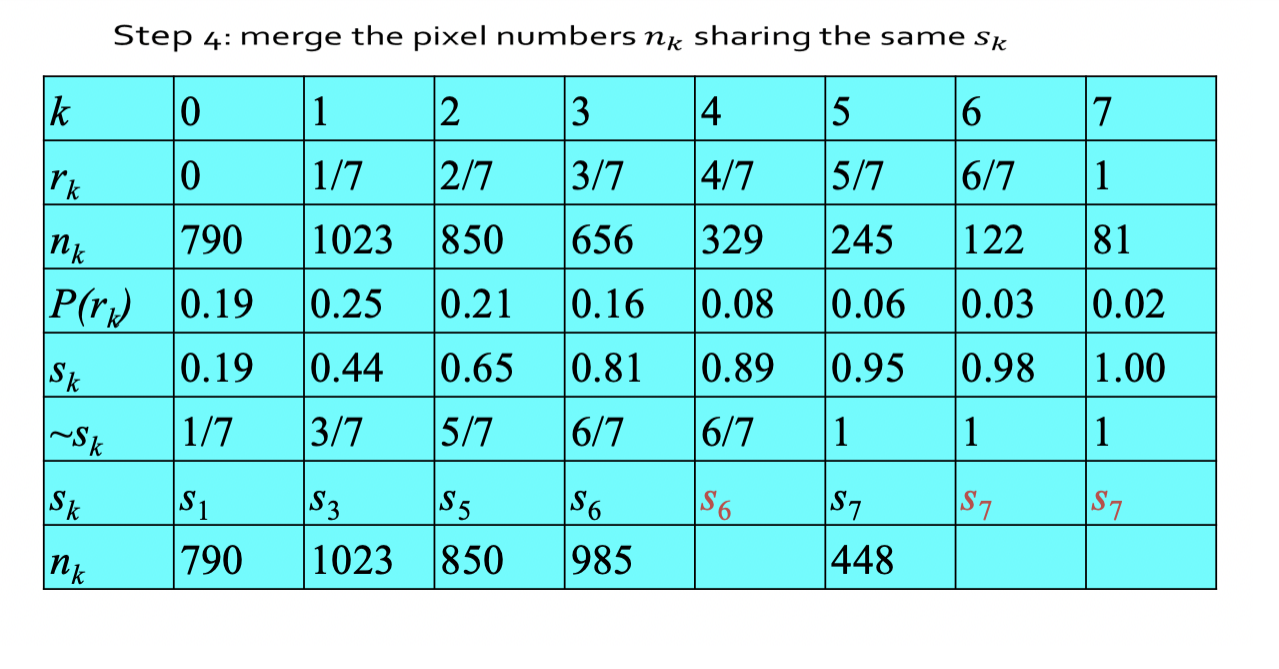
image-20240106104627681

image-20240106104618142

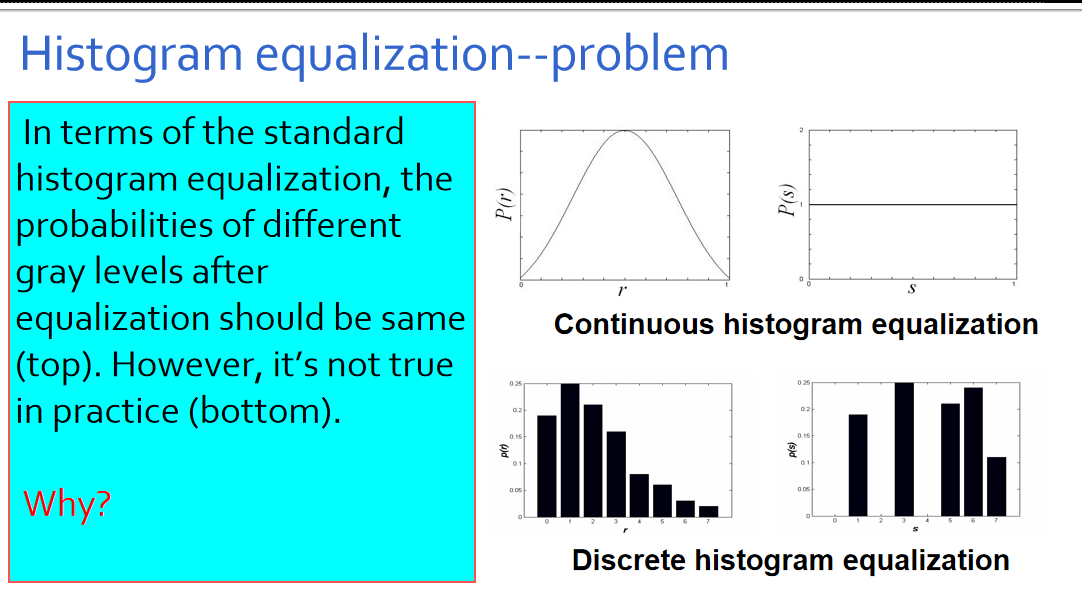
直⽅图均衡化的问题 image-20240106105439263

按照均衡化的要求，在均衡化后的结果直⽅图中，各灰度级发⽣的概率应该是相同的，如右上图所示连续灰度级均衡化结果那样。但是，右下图中离散灰度级均衡化后，各灰度级出现的概率并不完全⼀样，为什么？

步骤2中，所得的sk不可能正好等于8级灰度值中的某⼀级，因此需要就近归⼊某⼀个灰度级中。

这样，相邻的多个sk就可能落⼊同⼀个灰度级，需要在步骤3时将处于同⼀个灰度级的像素个数累加。因此，离散灰度直⽅图均衡化操作以后，每个灰度级处的概率密度（或像素个数）并不完全⼀样。

直⽅图的匹配(Histogram fitting)

  • 所谓直方图匹配，就是修改一幅图像的直方图，使得它与另一幅图像的直方图匹配或具有一种预先规定的函数形状。

  • 直方图匹配的目标，是突出我们感兴趣的灰度范围，使图像质量改善

  • 利用直方图均衡化操作，可以实现直方图匹配过程。

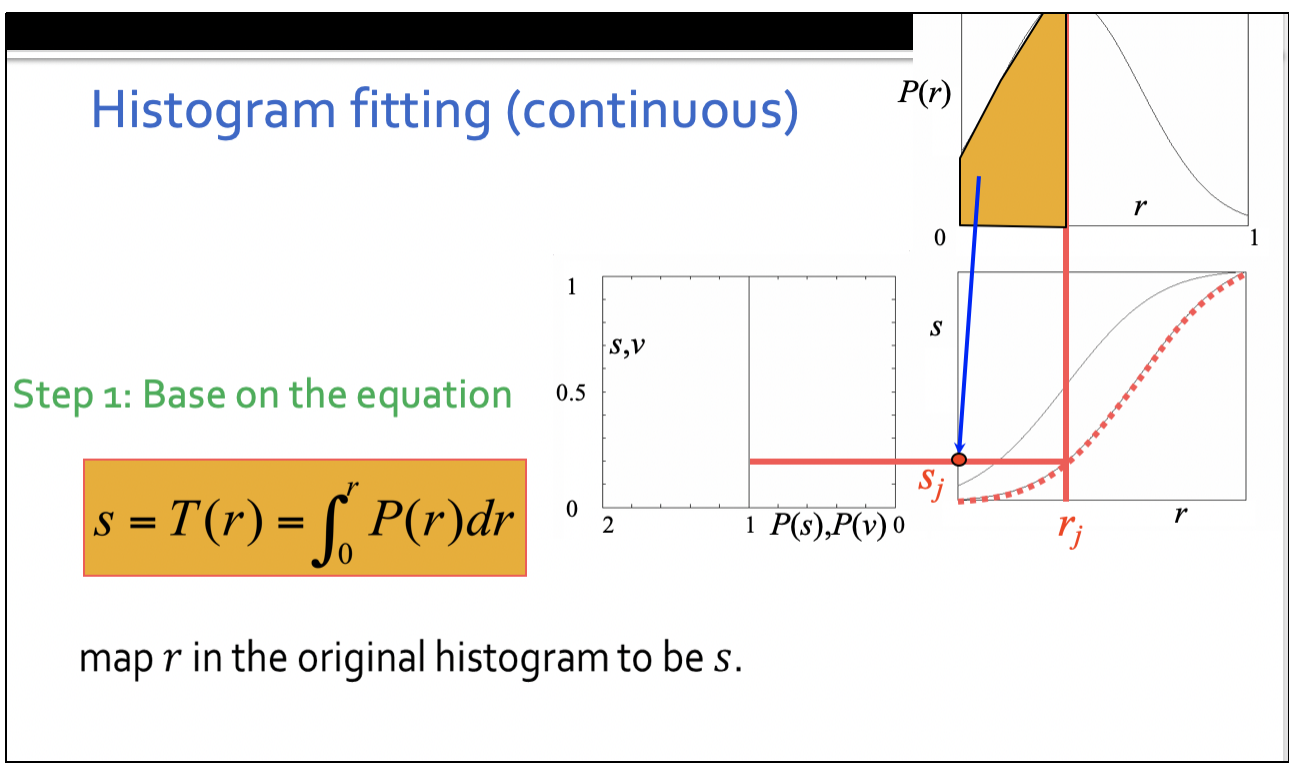
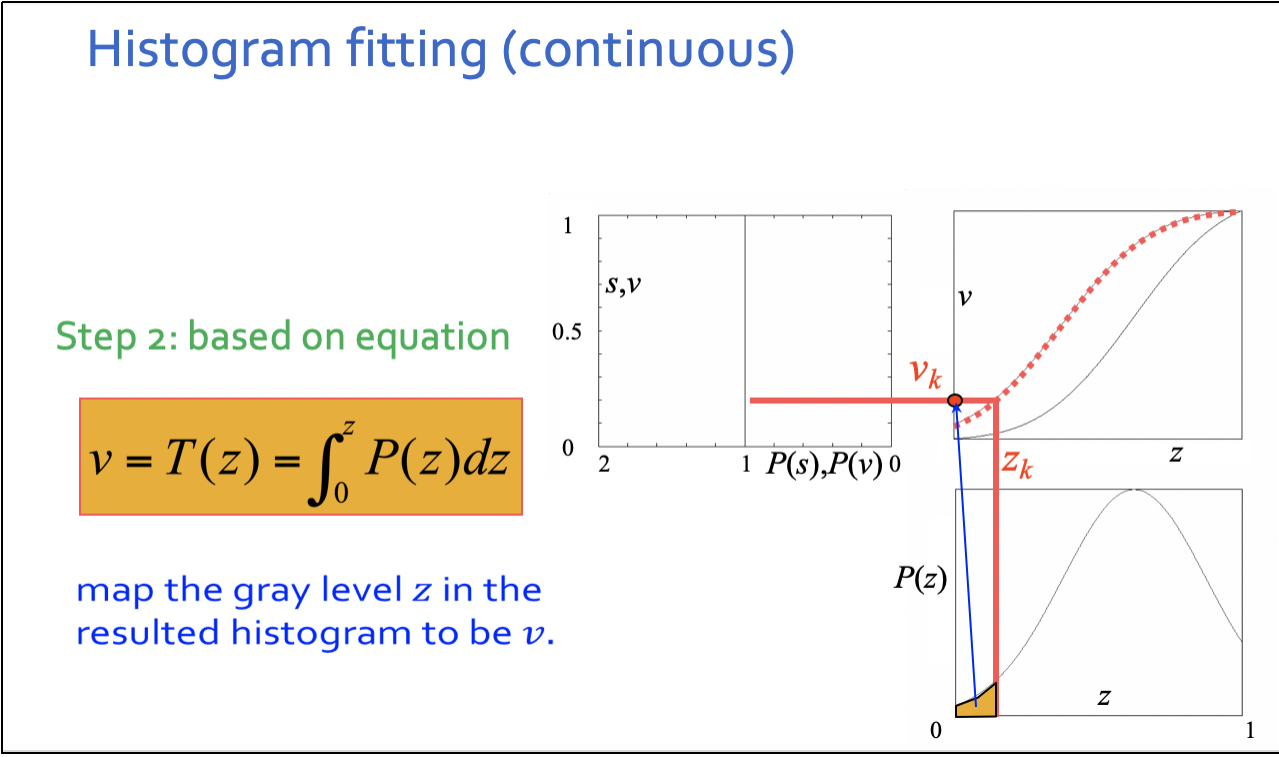
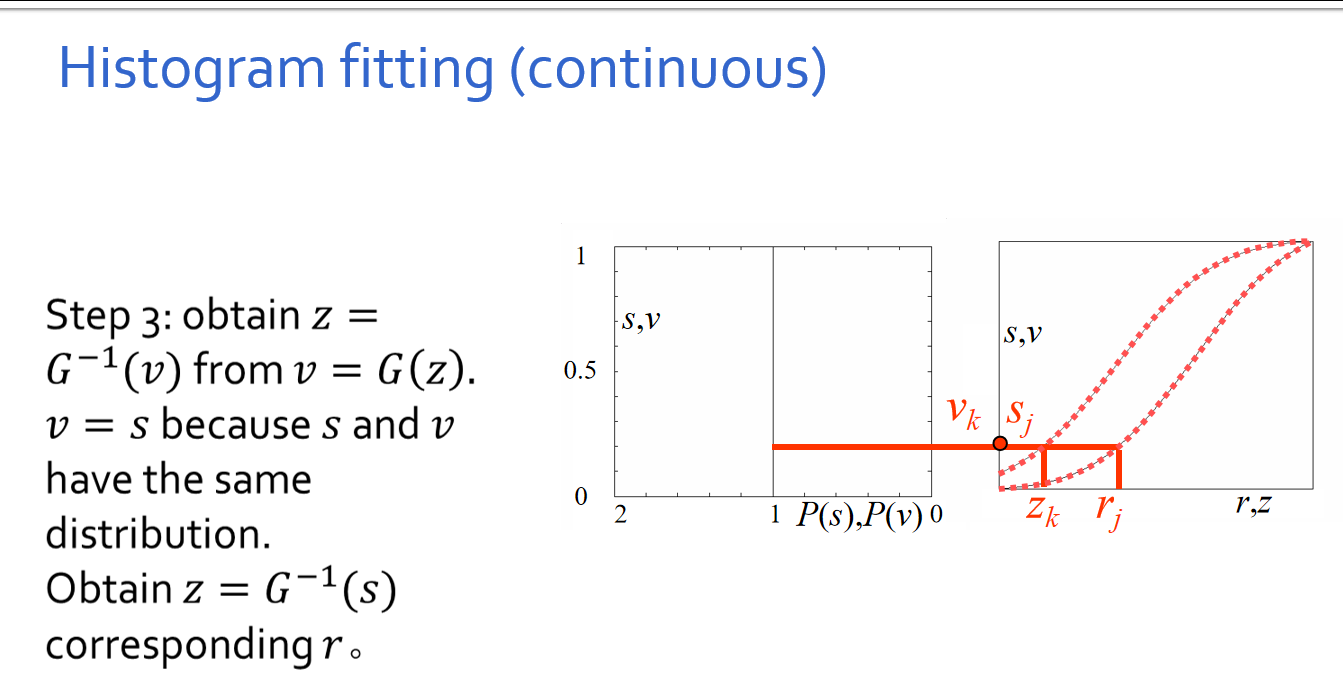
⽬的，把直⽅图A转换到B

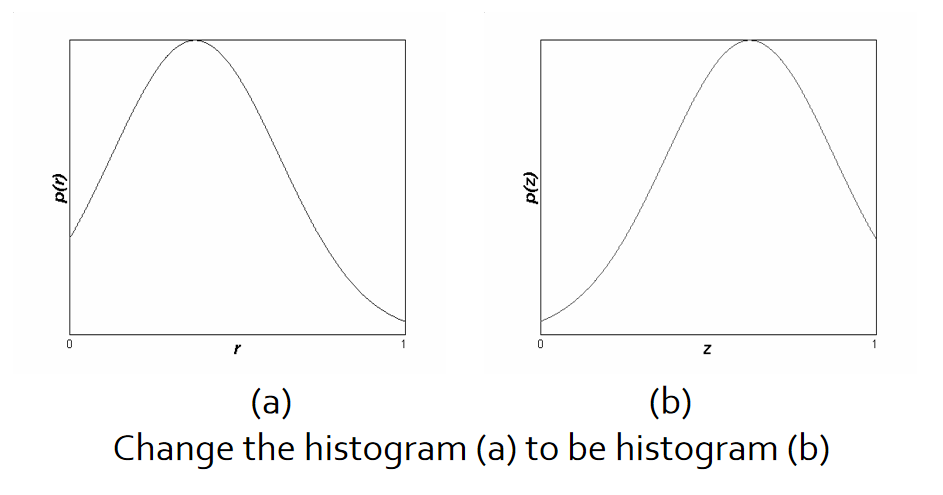
image-20240106110214840

第⼀步，通过直⽅图 均衡化把r映射到s

image-20240106110348091

第⼆步，同理把灰度级z映射到v

image-20240106110339833

第三步,由v = G(z)得到z =G-1(v)。由于s和v有相同的分布，逐⼀取v = s，求出与r对应的z =G- 1(s)。

image-20240109211309870

简述版本：

在步骤1和2中，分别计算获得两张表（参⻅直⽅图均衡化中的算例），从中选取⼀对vk、 sj，使vk = sj，并从两张表中查出对应的zk、rj。这样，原始图像中灰度级为rj的所有像素都映射成灰度级zk，最终得到所期望的图像。

Ch4

** 各种变换的坐标公式要掌握

旋转以后产⽣空洞的插值⼿法

  1. ⾏插值——按顺序寻找每⼀⾏中的空洞像素，设置其像素值与同⼀⾏中前⼀个像素的像素值相同。

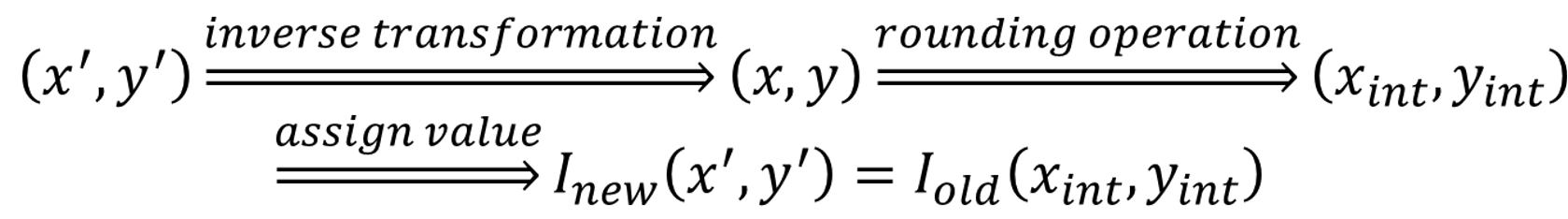
  2. 最近邻插值---为了计算⼏何变换后新图像中某⼀点P’处的像素值，可以⾸先计算该⼏何变换的逆变换，计算出P’所对应的原图像中的位置P。通常情况下，P的位置不可能正好处在原图像的某⼀个像素位置上（即P点的坐标通常都不会正好是整数）。寻找与P点最接近的像素Q，把Q点的像素值作为新图像中P’点的像素值。 image-20240106111334032

当图像中包含明显的几何结构时，结果将不太光滑连续，从而在图像中产生人为的痕迹。

  1. ⼀维线性插值

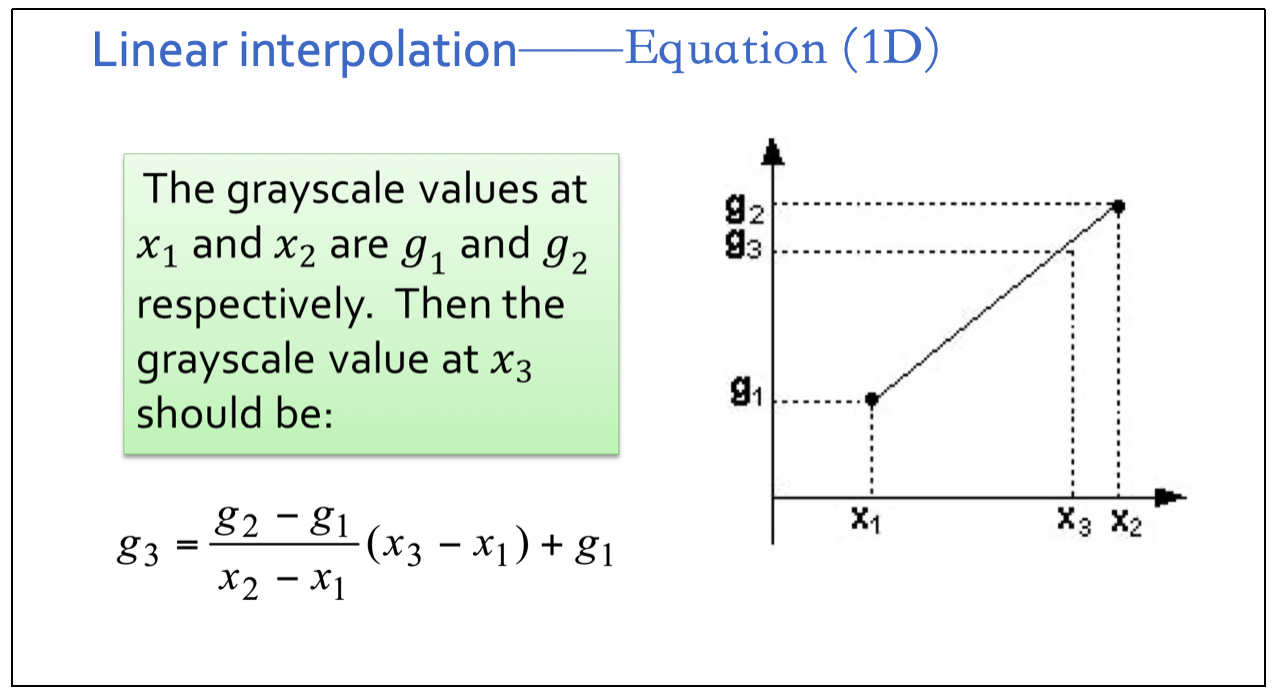
image-20240106111003106

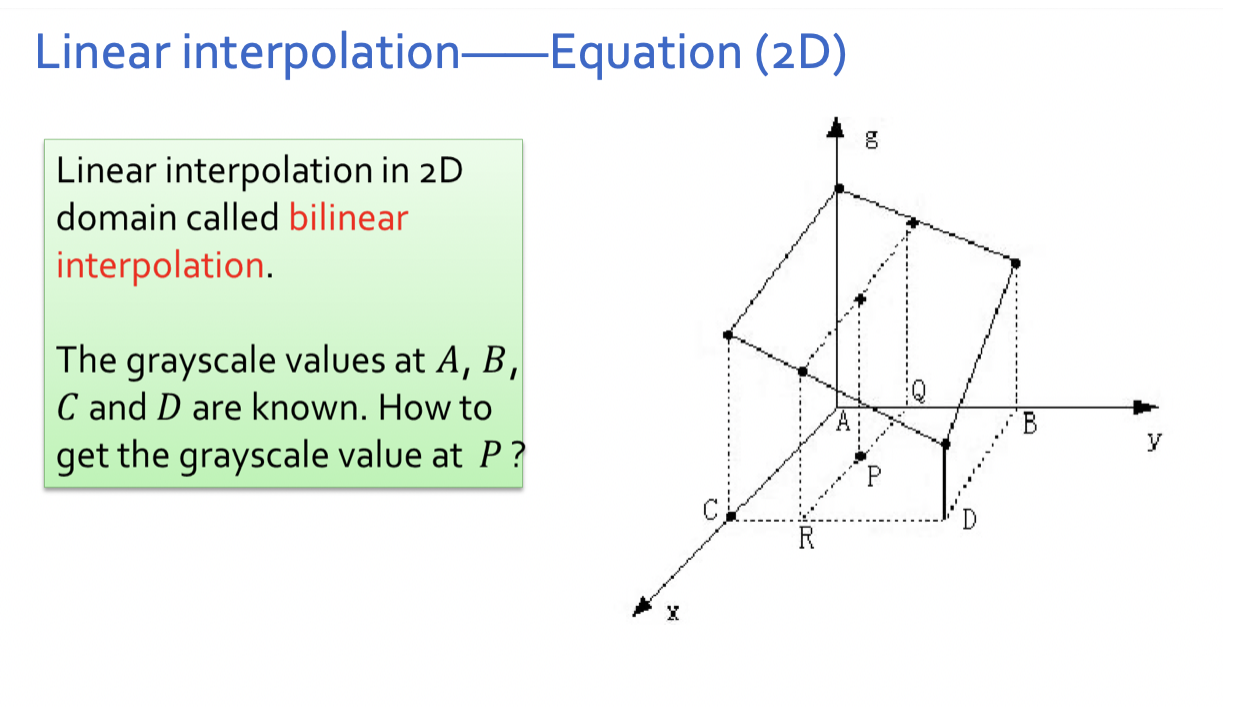
  1. 双线性插值

已知图像的正⽅形⽹格上四个点A、B、C、D的灰度，求P点的灰度。

image-20240106111028893

定义双线性方程g(x,y)=ax+by+cxy+d 。
分别将A、B、C、D四点的位置和灰度代入方程，得到方程组。
解方程组，解出a、b、c、d四个系数。
将P点的位置代入方程，得到P点的灰度。

Morph图像的变形

这里讨论的Morph变形不同于一般的几何变换(Warp)。 Morph变形指景物的形体变化，它是使一幅图像逐步变化到另一幅图像的处理方法。 这是一种较复杂的二维图像处理，需要对各像素点的颜色、位置作变换。 变形的起始图像和结束图像分别为两幅关键帧，从起始形状变化到结束形状的关键在于自动地生成中间形状，也即自动生成中间帧。

Change A to B

image-20240106111829884

⼤⼩相同的两幅图的转换作静态变换。从⼀幅图a逐渐变化成第⼆幅图b。原理：让图a中每个像素的颜⾊，逐渐变成图b相同位置像素的颜⾊。

⽅法：根据变换的快慢，设置相应的步⻓，将图a每⼀点的RGB逐渐变成图b相同位置象素的 RGB。可以选择等⽐或等差的⽅式，或其它⽅式让：ra-->rb。

对于灰度图像，可以直接⽤等⽐或等差级数定义步⻓，使颜⾊从原图变到⽬标图。

* 应用 Morph 表情匹配

Assumption: Human faces have approximately the same normals

image-20240106113124411

image-20240109212128899

image-20240109212308410

image-20240106112921229

Ch5

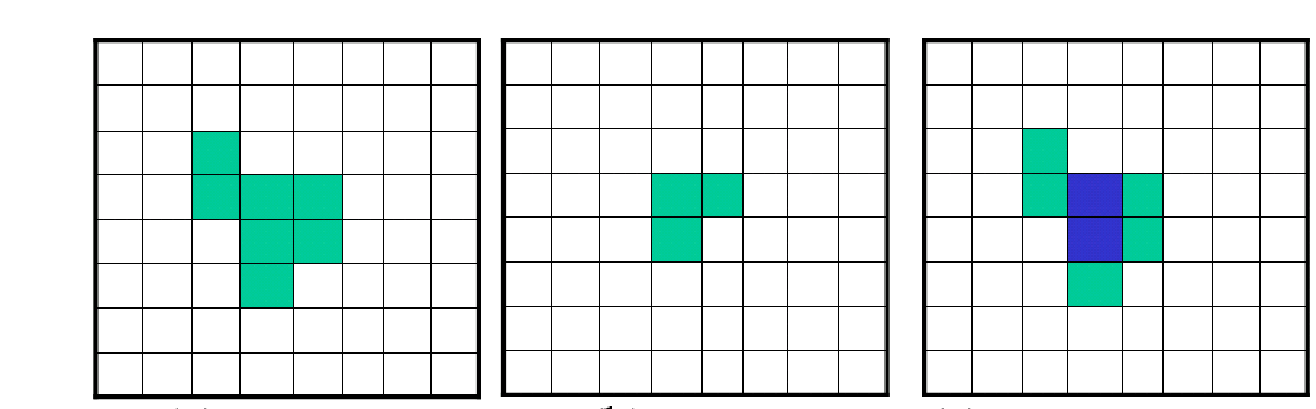
⼀维卷积

卷积本质上等同于计算图像像素的加权和。下面的例子要掌握

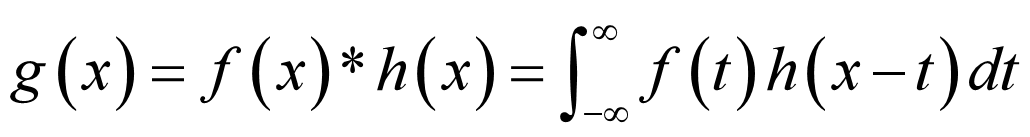
image-20240106113419115

  • 它表示两个函数的卷积可以转化成乘积的积分来计算。通常将f(x)称为输入函数，将h(x)称为卷积函数。

这⾥要注意的是得到的g(x)的定义域为[0,799]

image-20240106114110284

步骤1： 将卷积函数h(t)关于原点进行镜像映射（倒转），得到h(-t)。 image-20240106114037929

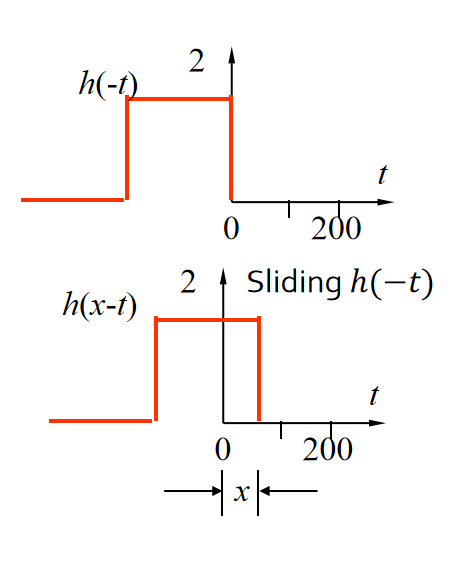
步骤2： 将倒转过的函数h(-t)滑过f(t)，这要增加一个常数位移x到h(-t)，即变成h(x-t)。 image-20240106114123749

步骤3： 对每一个样本点t （t = 0, 1, 2, 3, …, 399）都计算乘积f(t)h(x-t)，然后将这些乘积相加后除以常数M（=400），就得到在位移x下的卷积。

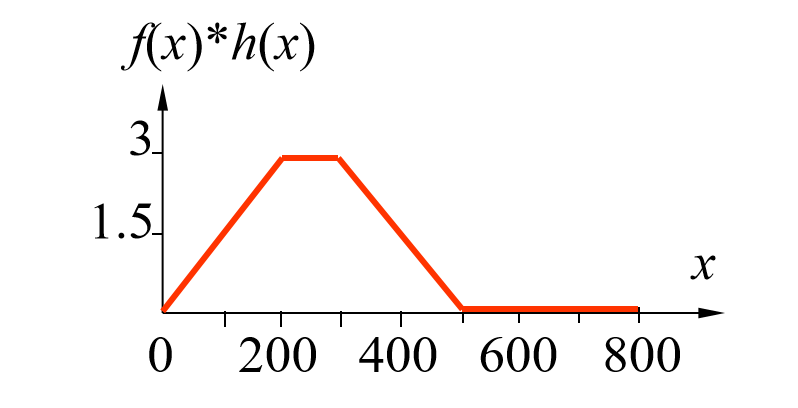
image-20240106114136148

步骤4： 对有效范围内的所有位移x均计算一个卷积，这样，所有这些值就形成了一条曲线。

Sharping filter 拉普拉斯

微分算子是实现锐化的工具，其响应程度与图像在该点处的突变程度有关。微分算子增强了边缘和其他突变（如噪声）并削弱了灰度变化缓慢的区域。

  • 基于一阶微分的图像增强——梯度法

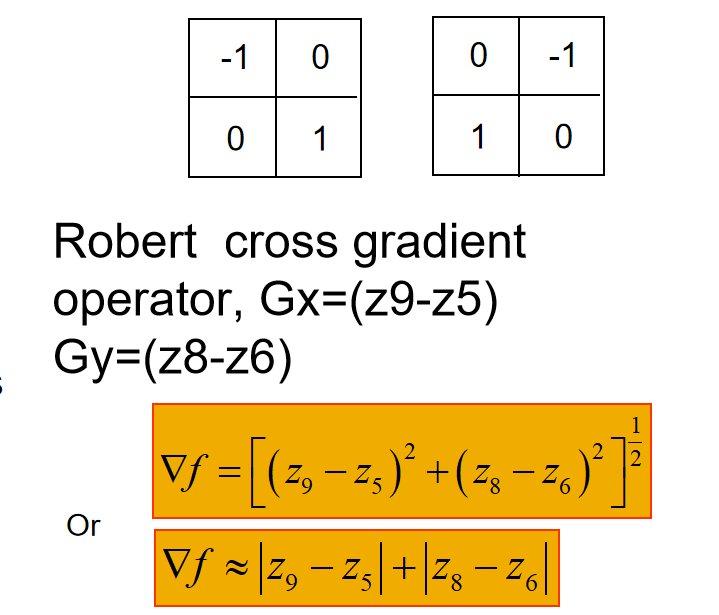
  • 基于二阶微分的图像增强——拉普拉斯算子

左侧为正常的算子，右侧为extending one

image-20240110093543487

当拉普拉斯滤波后的图像与其它图像合并时（相加或相减），则必须考虑符号上的差别 将原始图像和拉普拉斯图像叠加在一起的简单方法可以保护拉普拉斯锐化处理的效果，同时又能复原背景信息。

image-20240106133643581

平滑空间滤波 | 低通滤波

空间滤波

搞清楚，均值滤波和中值滤波不是⼀回事，均值滤波是⾼斯滤波的⼀种特例，⾼斯滤波是⼀种低通滤波。

当发现图像中有太多的伪影或噪声时，可以对图像进⾏平滑处理，抑制噪声，减少伪影。 然⽽，平滑操作会使图像变得模糊。

Linear smoothing filter

  • 线性

Statistical sorting filter

  • 非线性
  • 常用n×n的中值滤波器去除那些相对于其邻域像素更亮或更暗，并且其区域小于n2/2（滤波器区域的一半）的孤立像素集。

image-20240106114807441

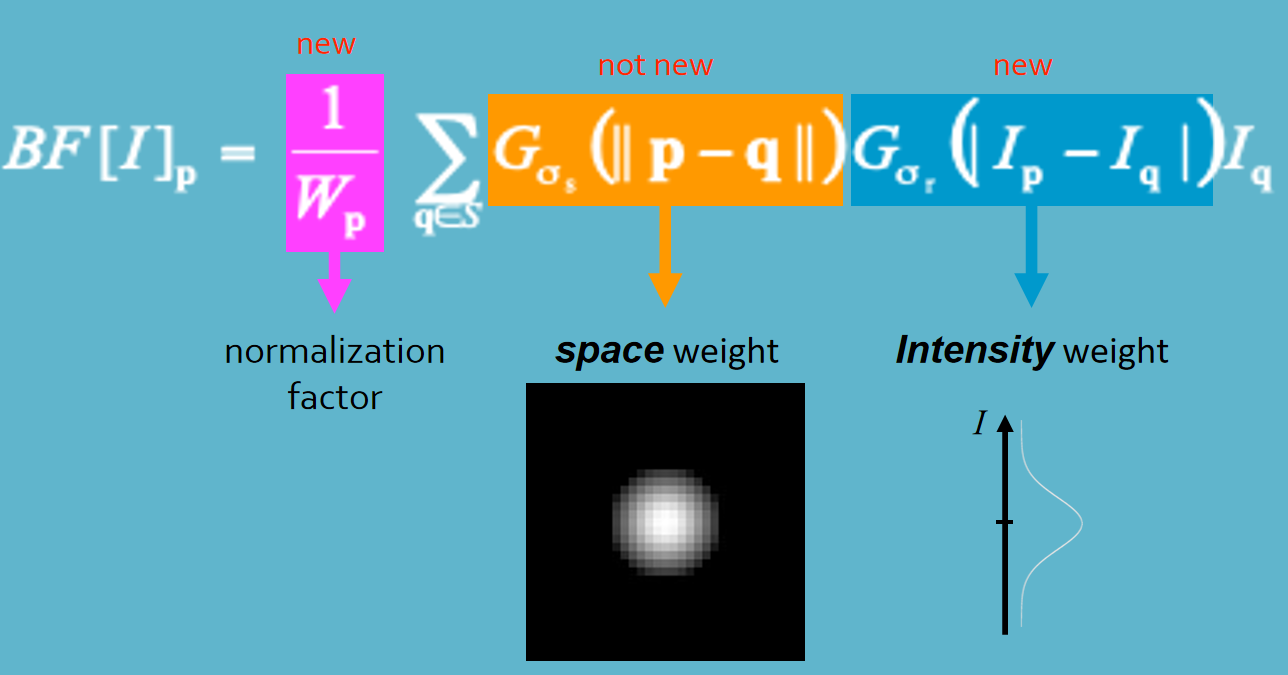
双边滤波的general idea

⼀幅图像有两个主要特征

空间域S，它是⼀幅图像中可能位置的集合。 这与分辨率有关，也就是图像中的⾏数和列数。

强度域R，是可能像素值的集合。 ⽤来表示像素值的位数可能会变化。 常⻅的像素表示形式是⽆符号字节(0到255)和浮点数。

⾼斯滤波只考虑了前⼀个域。（把$r$拉到正无穷，那么将变成高斯模糊）

image-20240106130759819

双边滤波公式每个的含义

image-20240106131136668

From GPT 双边滤波（Bilateral Filter）是一种常用的图像处理技术，它可以在保持边缘清晰的同时对图像进行平滑处理。双边滤波器的两个参数分别是空间域标准差（$\sigma_s$）和灰度值域标准差（$\sigma_r$）。

  • $\sigma_s$：控制了在空间上进行平滑的范围。较大的 $\sigma_s$ 值意味着更广泛的空间范围内的像素将被考虑，从而产生更大范围的平滑效果。
  • $\sigma_r$：控制了对灰度值进行平滑的范围。较大的 $\sigma_r$ 值意味着对于灰度值差异较大的像素，其权重会更大，这可以帮助保持图像的边缘信息。
  • 增大 $\sigma_s$ 会导致更大范围的像素被考虑在内，因此产生更大范围的平滑效果，但也可能导致图像失真。而增大 $\sigma_r$ 会使得对灰度值差异较大的像素有更大的权重，因此可以更好地保留图像的边缘信息，但也可能导致边缘细节不够平滑。 因此，合理选择 $\sigma_s$ 和 $\sigma_r$ 的值对于获得满意的双边滤波效果非常重要。

How to set （From PPT）

  • $\sigma_s$ : 与窗口大小有关
  • $\sigma_r$ : 与边缘振幅成正比
  • 与分辨率和曝光无关

双边滤波因为引⼊了快速傅⾥叶变化才实现加速

消除噪音

image-20240106131809539

Guided filter为什么⽐双边滤波好，以及Guided filter的优点

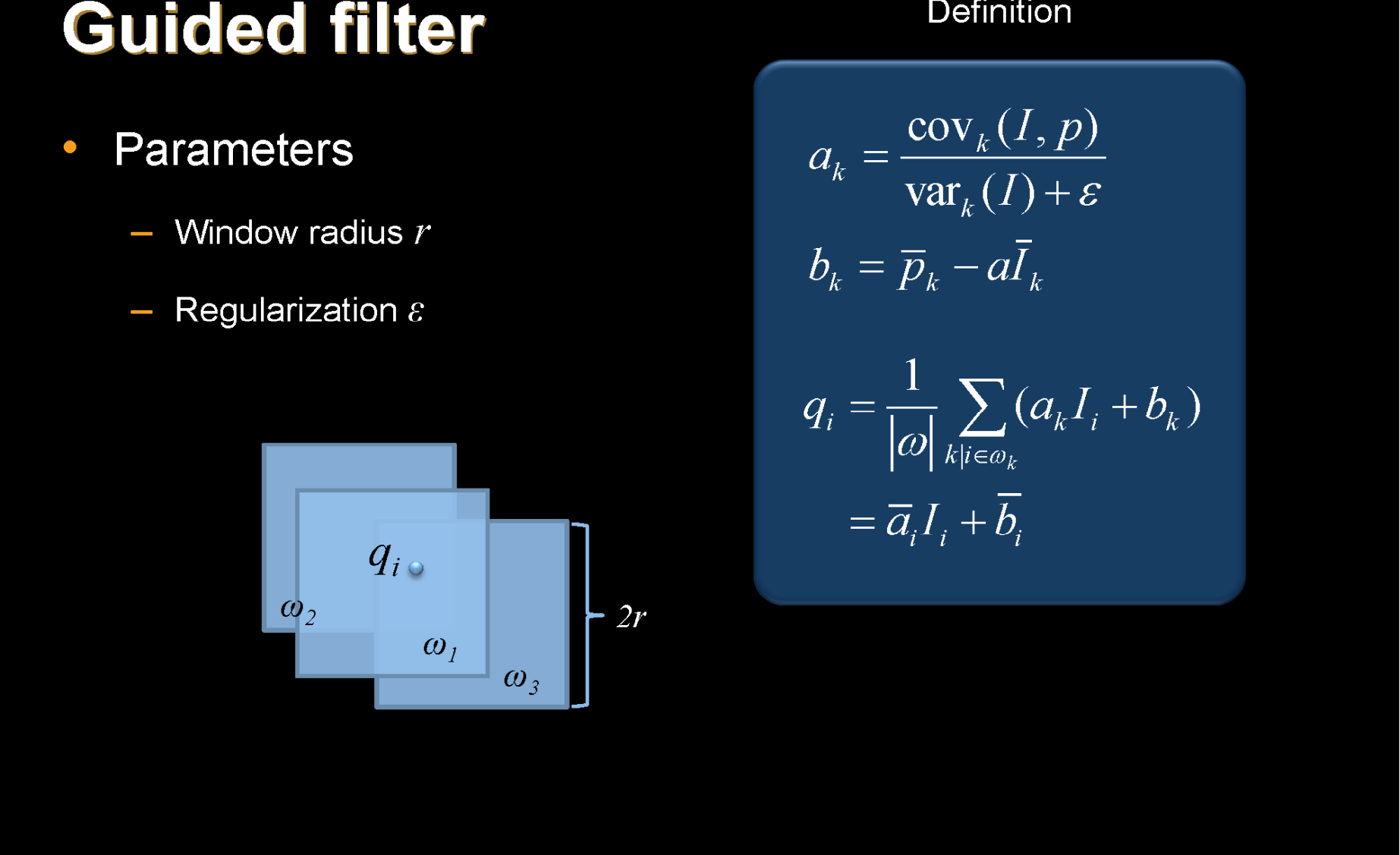
image-20240106141608217

Regularization 越大，保边能力越强

因为Guided filter考虑了保梯度，不会造成梯度的逆转，但是双边滤波会产⽣梯度的逆转，因为双边保的是difference的绝对值，⽽不是⽅向。

image-20240106141219348

移除不需要的频率

image-20240106141417318

SNF 稀疏范数滤波

image-20240106142534614

  • p>1不能防止梯度逆转，p<1才可

证明：p = 1，中值滤波；p=2，高斯滤波（均值）

因为 SNF 的微分是非局部的，他不那么可能陷入梯度下降的情况

image-20240106143130917

Ch6

FT 傅里叶变换

  • 下面为FT的去噪

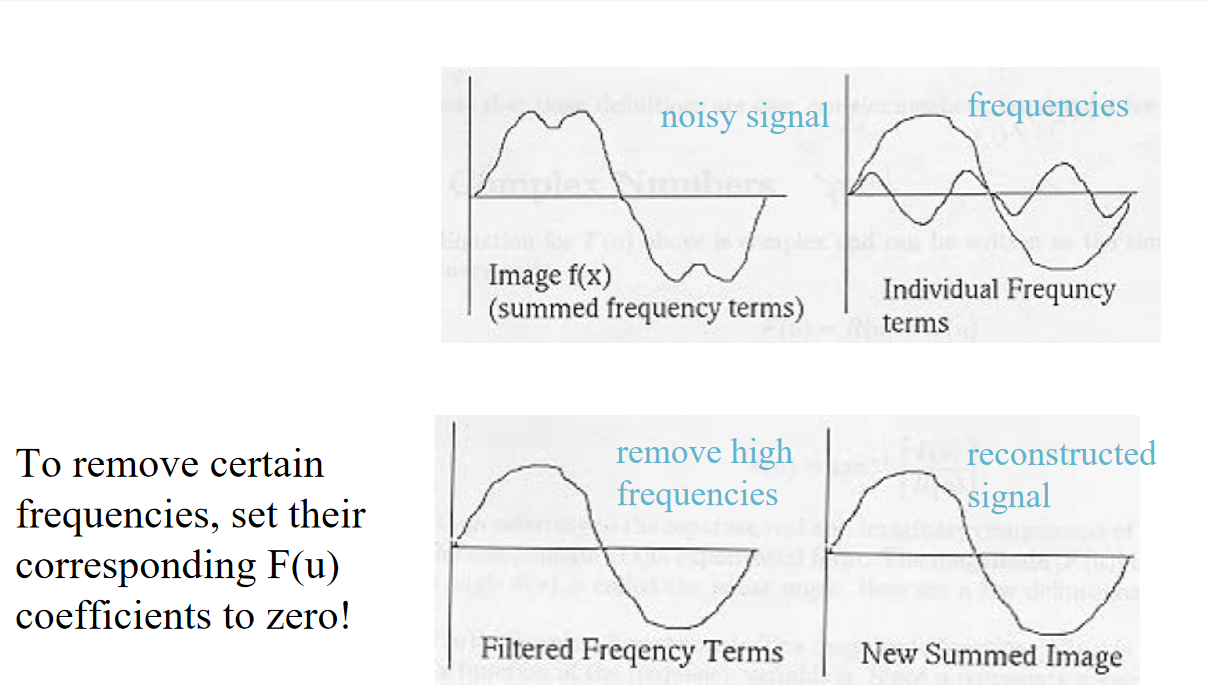
image-20240106143751987

image-20240106144433097

1. 进行傅里叶变换
2. 在变换后的X（t）中进行滤波
3. 进行逆傅里叶变换

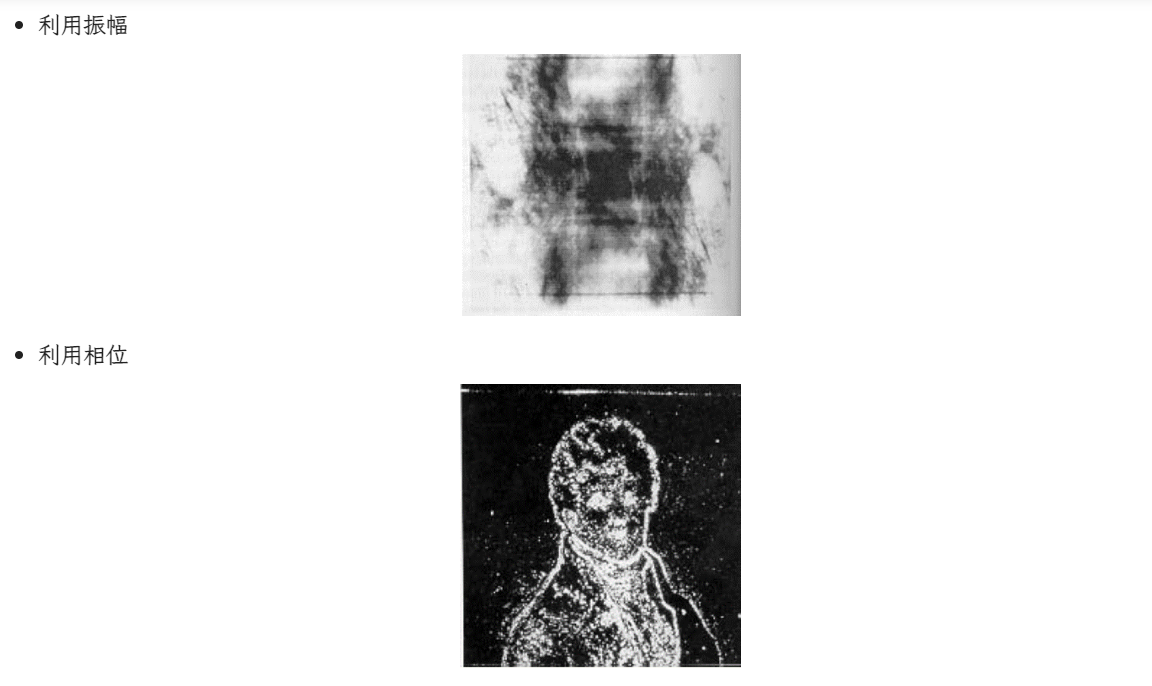
DFT

  • 相位可以用来传递结构信息，幅值不行 image-20240106145832541

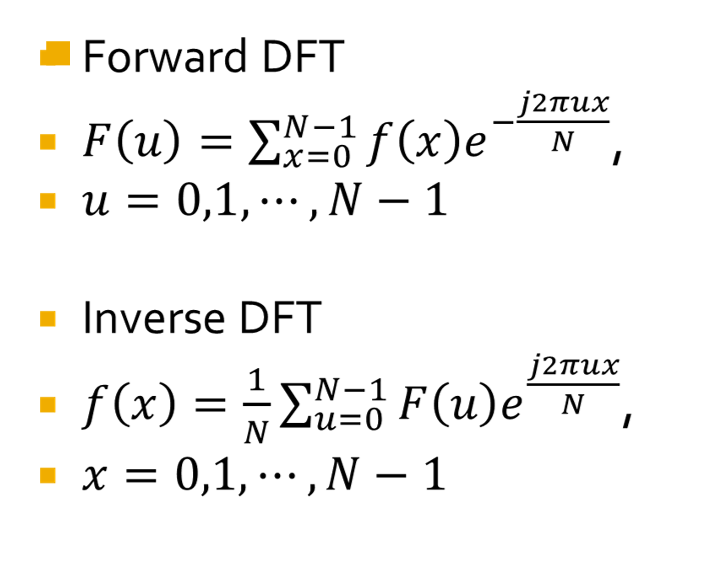
image-20240106145320336

FFT 快速傅里叶变换

  • 将原始的 N 点序列依次分解为一系列短序列；
  • 求出这些短序列的离散傅立叶变换；
  • 组合出所需的变换值；
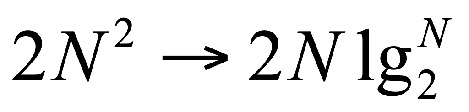
  • 计算量（乘除法）：image-20240106145344721

FFT的推导

image-20240106145440924

image-20240106145453829

image-20240106145505200

Ch7

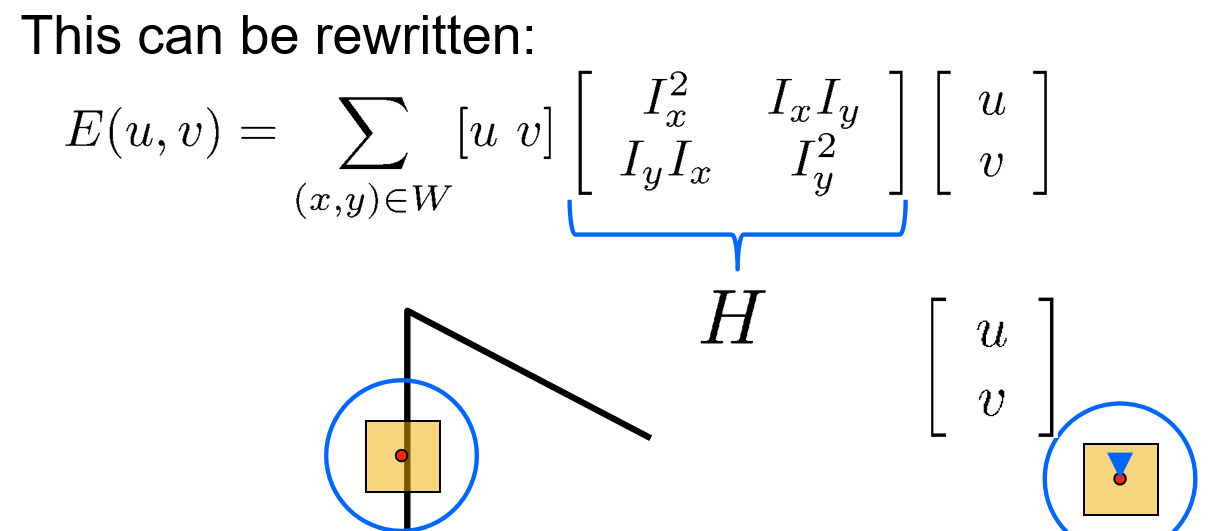
角点特征检测

我们考虑一个小窗口的像素

  • flat: 在任何方向都不会有像素的改变
  • egde: 沿着边的方向不会有像素的改变
  • corner: 在任何方向都会有明显的改变

特征

  1. 旋转不变性
  2. 缩放会具有影响

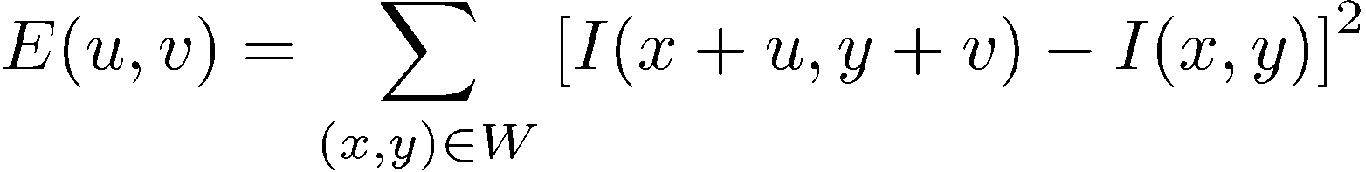
Detect the Error 使用SSD suming up the Square Differen'vce image-20240106150344733

image-20240107165000283

image-20240106150505828

image-20240106150549194

image-20240106150720801

image-20240106151408090

我们可以在蓝色的圆圈内移动window，最大和最小的E的位置如何取得依赖于H的特征向量

不变性

image-20240107165235185

Harris Laplacian

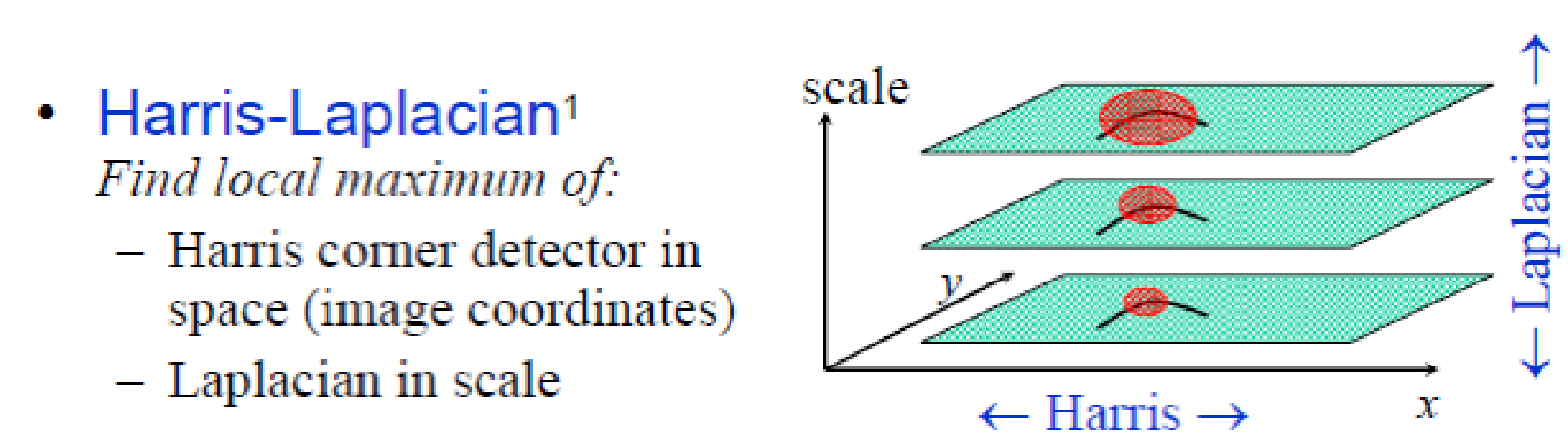
image-20240107165732596

不同维度计算方法不一样

  • 初始化：多尺度的 Harris corner detection(改变清晰度后，单独找角点) 只有在任何尺度上都是角点的点，才能被保留
  • 基于拉普拉斯算子，进行尺度选择。对一个位置，哪一个尺度上拉普拉斯值最大，将这个位置和尺度作为角点。（唯一性，在这个尺度上是极大值，那么在另一个尺度上也是极大值，只是极大值的数值可能不同）

Laplacian-of-Gaussian = "blob" detector 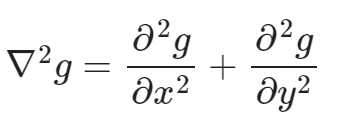image-20240107170017741

在图像中给定的一个点，我们定义拉普拉斯响应值达到峰值的尺度为特征尺度(characteristic scale)

SIFT

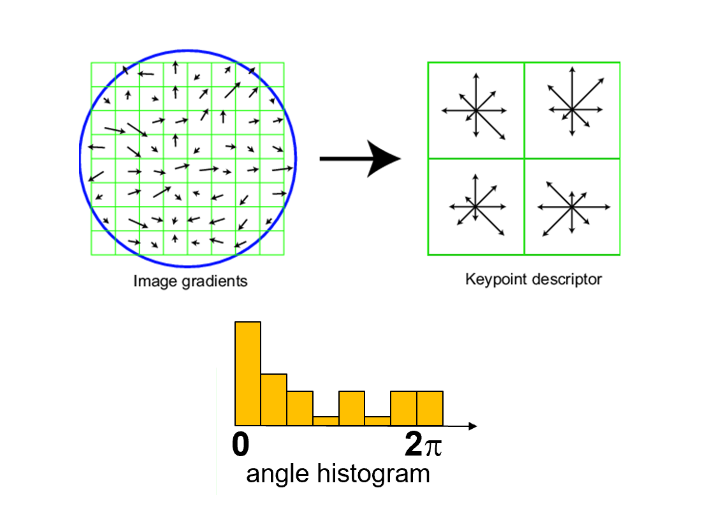
image-20240107170740388

  • 在检测到的特征角点周围选取 16×16 的方形窗口
  • 计算每个像素的边的朝向(梯度的角度- 90°)
  • 剔除弱边缘(小于阈值梯度幅度)
  • 创建剩下边的方向的直方图

完整版：

  • 将 16×16 的窗口 划分为 4×4 的网格
  • 对每个网格计算其方向直方图
  • 16 cells * 8 orientations = 128 dimensional descriptor(128 维向量)

SIFT为什么能做到旋转不变性

SIFT 特征：旋转不变性 根据其主要梯度方向(dominant gradient orientation)旋转 patch, 这样可以使他处于规范方向

SIFT为什么能做到尺度不变性

  1. 在检测特征附近创建⼀个16*16的正⽅形窗⼝

  2. 对于每个像素计算其边缘⽅向

  3. 除去弱的边

  4. 对剩下的边创建⼀个直⽅图

SIFT的128维的特征是哪来的

16*16的窗⼝分为16个4*4的⼩块，每个⼩块有⼋个⽅向，所以有128维的特征

SIFT的应⽤

图像的识别与拼接

SIFT的优缺点

优点：

  1. 具有尺度、 旋转、 亮度不变性

  2. 在局部块上有⾼度独特和描述性

  3. 在刚性对象表示中特别有效

缺点： 

  1. 提取时间过⻓

  2. 对于⾮刚性对象的表现较差

  3. ⽆法在严重仿射失真中⼯作

SURF

image-20240107171649077

RANSAC的流程

拟合数学模型并识别数据中的离群值的迭代方法。它的主要应用是在计算机视觉和图像处理领域，用于估计模型参数，例如拟合线、平面或其他几何形状，并排除异常值的影响。

  1. 随机抽样：首先从数据集中随机选择一定数量的数据点来构建候选模型。

  2. 模型拟合：使用选定的数据点来拟合模型（例如，拟合一条直线以适应选定的两个点）。

  3. 内点筛选：对于剩余的数据点，检查它们是否与当前拟合的模型一致。如果一个数据点与当前模型一致（例如，距离在一定阈值内），则将其标记为“内点”，否则标记为“外点”。
  4. 评估模型：计算模型适应数据的度量，例如符合内点的数量。
  5. 重复迭代：重复上述步骤多次（通常是几十甚至几百次），选择产生最大内点数的模型。

  6. 模型验证：最终模型需要经过验证，以确保其在整个数据集上的性能。

  7. 随机选择种子点作为转换估计的基础

  8. 计算种子点之间的变换
  9. 找到这次变换的 inliers
  10. 如果 inliners 的数目足够多，那么重新计算所有 inliners 上的最小二乘法估计
  11. 回归之后再计算 inliners 如此往复，继续调整。如果没有调整那我们可以停止循环。最终使得回归出的线达到最多的 inliners.

w=0.8, 模型取点数为3，问最少要取几个点才能保证概率>95%RANSEC收敛

image-20240108174307329

图像拼接的主要流程

image-20240107181501952

拉普拉斯金字塔

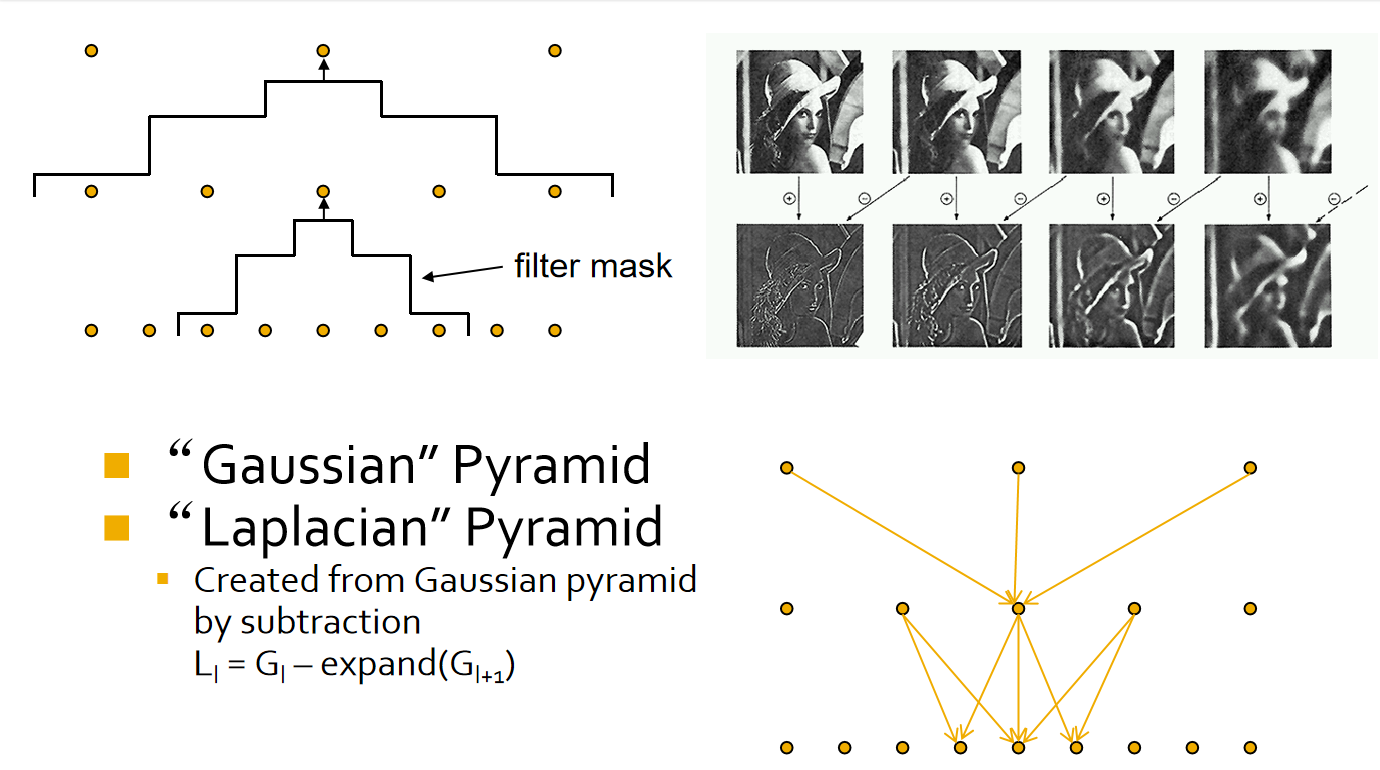
image-20240107182435884

拉普拉斯金字塔是通过高斯金字塔计算得到的。下面是获得拉普拉斯金字塔的步骤：

1. 首先，通过对原始图像进行重复采样和高斯模糊操作，得到高斯金字塔。高斯金字塔是由一系列分辨率逐渐减小的图像组成的，每一层图像都是通过对上一层图像进行降采样和高斯模糊得到的。

2. 接下来，通过对高斯金字塔进行上采样，得到一个比原始图像大一倍的图像。然后，将上一层高斯金字塔的图像减去上采样得到的图像，得到当前层的拉普拉斯图像。

3. 重复进行上述步骤，直到达到金字塔的顶层。

通过这个过程，我们可以得到拉普拉斯金字塔，它是由一系列图像组成的，每个图像都代表了原始图像在不同空间尺度上的细节信息。

Ch8

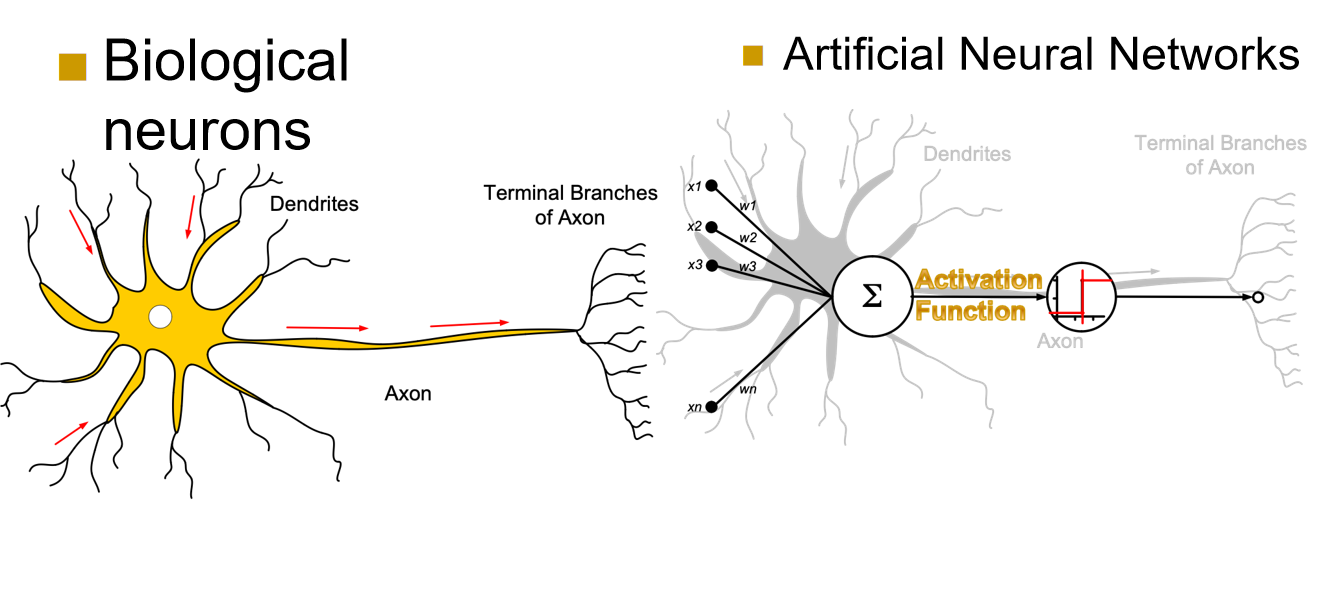
神经元

image-20240107184150172

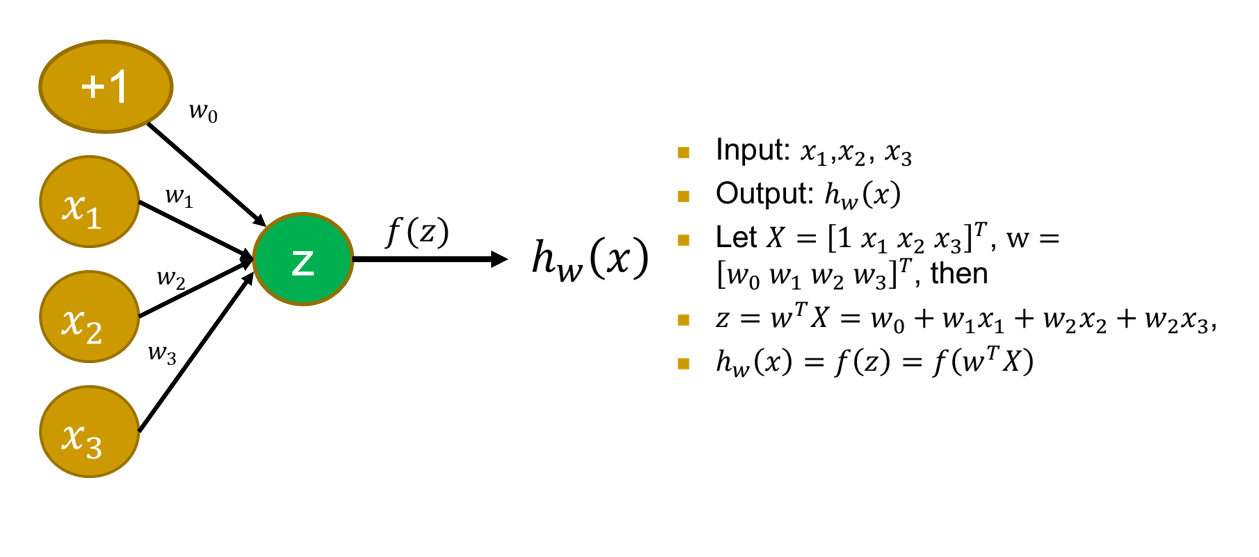
image-20240107184219873

BP算法

  • BP算法解决的是多重神经网络的求解过程（帮助理解）
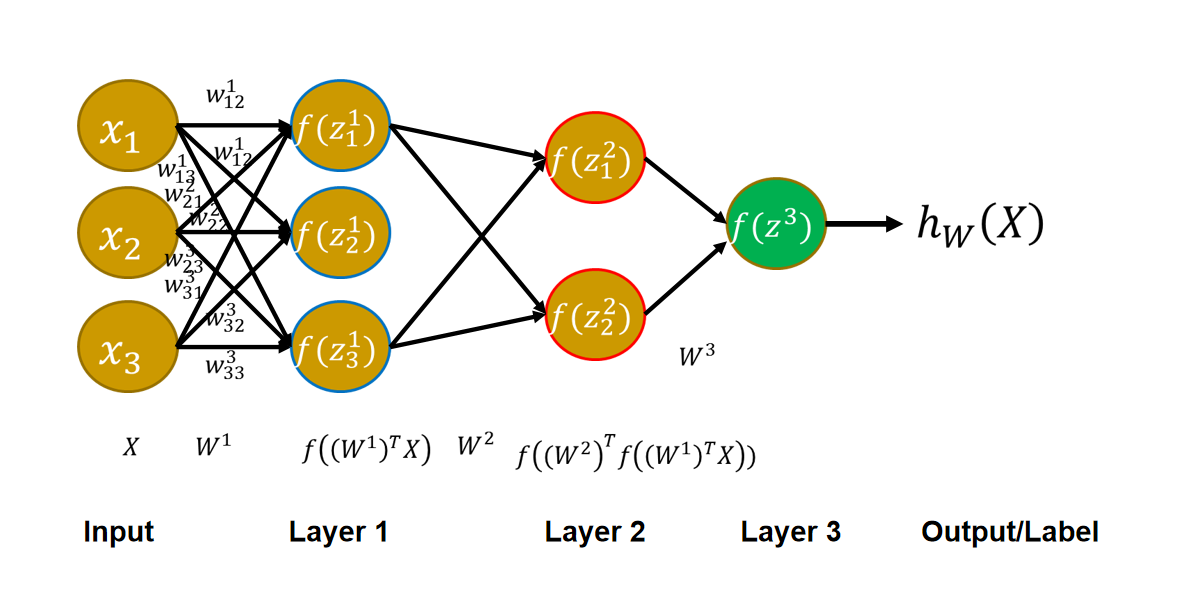
  • image-20240107184424232

image-20240107184339986

image-20240107184822917

​ 不断重复，直到E小于一个阈值

为什么加入卷积核，好处

加入卷积核有助于减少计算量，这主要体现在两个方面：

  1. 参数共享： - 卷积核的参数是共享的，这意味着在整个输入数据上使用相同的卷积核进行特征提取。 因此，无论输入数据的大小如何，卷积核的参数数量都保持不变。这种参数共享减少了需要训练的参数数量，从而降低了模型的复杂性。
    • 举例来说，假设输入数据是一个图像，如果我们使用大小为3x3的卷积核进行特征提取，无论图像的尺寸如何，卷积核的参数数量都是固定的，因为卷积核在整个图像上共享参数。这种参数共享大大减少了需要训练的参数数量，降低了计算成本。
  2. 稀疏交互： - 卷积操作是局部连接的，每个输出元素仅与输入的局部区域有关。这种稀疏交互使得模型更具有效性，因为在卷积操作中，只有卷积核覆盖到的区域才会参与计算，而其他区域则不会影响输出结果。
    • 举例来说，假设输入数据是一个大尺寸的图像，而卷积核的大小相对较小，那么在卷积操作中，每个卷积核只需要与输入数据的一个小区域进行交互，而不需要考虑整个图像。这种稀疏交互减少了需要处理的数据量，从而降低了计算成本。 因此，通过参数共享和稀疏交互，加入卷积核有助于减少计算量，降低模型的复杂性，并提高模型的计算效率。

计算

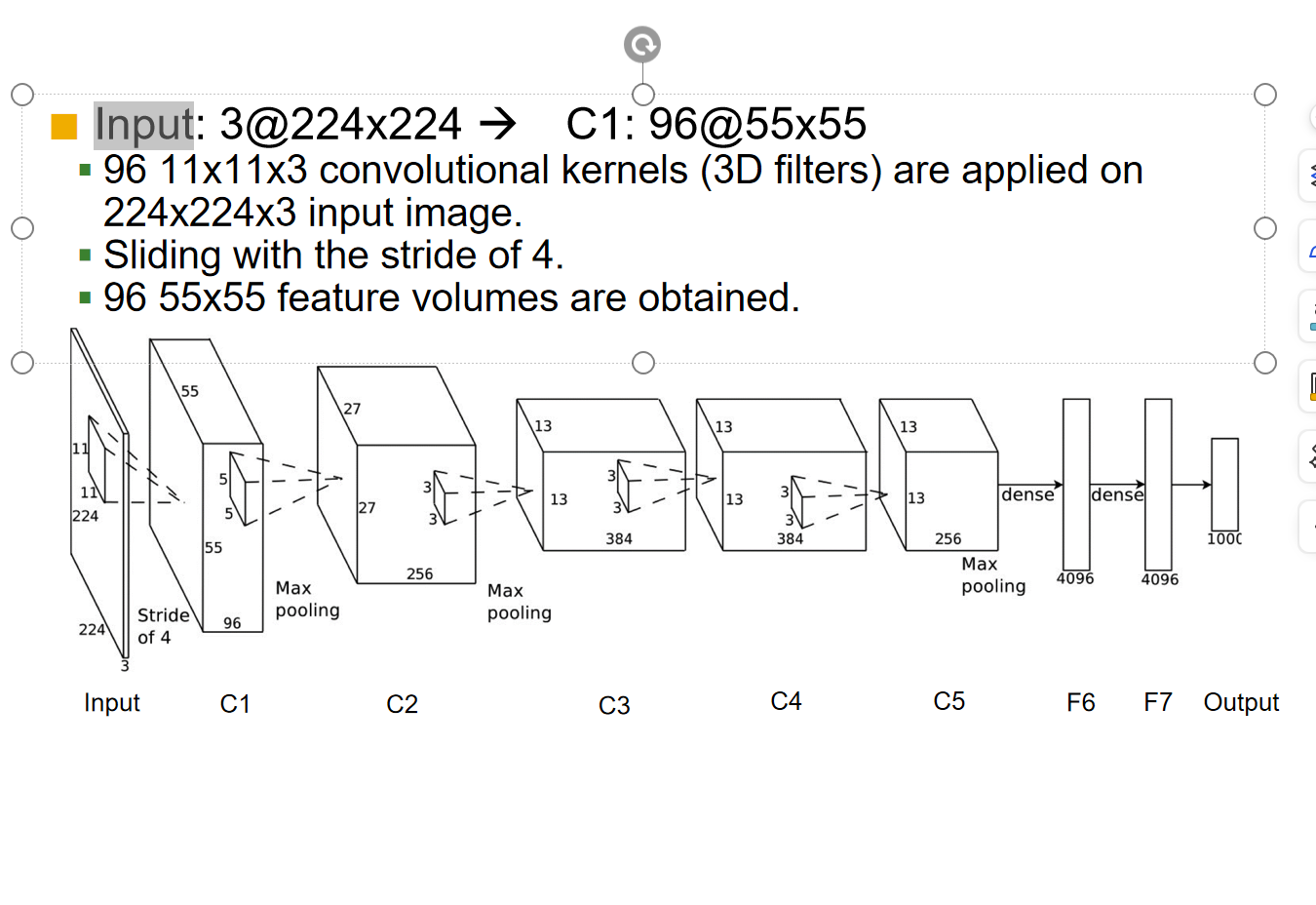
image-20240104151946690

From GPT 在这个例子中，我们可以计算每个卷积层输出特征图的尺寸。

假设输入特征图的尺寸为 $W_{\text{in}}\times H_{\text{in}}\times D_{\text{in}}$，卷积核的尺寸为 $F\times F\times D_{\text{in}}\times D_{\text{out}}$，步长为 $S$，填充为 $P$。

对于没有填充的情况，输出特征图的尺寸可以通过以下公式计算： $$ W_{\text{out}} = \frac{W_{\text{in}} - F}{S} + 1 $$ $$ H_{\text{out}} = \frac{H_{\text{in}} - F}{S} + 1 $$ $$ D_{\text{out}} = \text{卷积核的数量} $$

对于池化层，输出特征图的尺寸计算方式类似，但是是使用池化核的尺寸和步长进行计算。 在这个例子中，可以使用上述公式计算每个卷积层的输出特征图尺寸。

8332ec148f6f46310bf9bf73f617670

图像分类的区别

  1. 传统的图像分类：

  2. 传统的图像分类方法通常基于手工设计的特征提取器，例如SIFT（尺度不变特征变换）和HOG（方向梯度直方图）。这些特征提取方法依赖于领域专家对图像特征的理解，然后使用机器学习算法（如支持向量机、随机森林等）对提取的特征进行分类。

  3. 传统方法的局限在于特征提取需要依赖领域专家的知识，并且在复杂数据集上的泛化能力有限。

  4. 深度学习的图像分类：

  5. 深度学习方法，特别是卷积神经网络（CNN），能够端到端地学习图像的特征表示和分类器，无需手动设计特征提取器。深度学习方法通过学习从原始数据到目标标签的映射关系，可以自动地发现和提取特征，从而在图像分类任务上取得了显著的性能提升。

  6. 深度学习方法的优势在于它们能够从大规模数据中学习特征表示，无需依赖领域专家的先验知识，同时在处理复杂数据集时具有更好的泛化能力。

交叉熵

image-20240108202717382

  1. 代表含义： - 交叉熵是一种衡量两个概率分布之间差异的度量方式。在机器学习中，交叉熵常被用作损失函数，特别是在分类问题中。
  2. 损失$L$：
  3. 对于二分类问题，给定真实标签$y$和模型预测的概率分布$\hat{y}$，交叉熵损失$L$可以表示为：$L(y, \hat{y}) = -\left(y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})\right)$。
  4. 对于多分类问题，给定真实标签$y$和模型预测的概率分布$\hat{y}$，交叉熵损失$L$可以表示为：$L(y, \hat{y}) = -\sum_{i} y_i \log(\hat{y}_i)$，其中$y_i$表示真实标签的概率分布，$\hat{y}_i$表示模型预测的概率分布。 交叉熵损失函数在训练神经网络时经常被用作目标函数，因为它能够有效地衡量模型输出与真实标签之间的差异，并且能够促使模型产生更为准确的概率分布输出。

CNN

  • CNN 是少有的可以监督训练的深度模型，而且容易理解、实现。

为什么引⼊CNN可以⼤规模减少权数参数训练量

因为CNN通过

1） 局部连接（Local Connectivity） 卷积操作是局部连接的，这意味着每个神经元仅与输入的局部区域相连，而不是与整个输入相连。这种局部连接的方式也减少了需要训练的参数数量，因为每个神经元只需要学习与局部信息相关的权重。

2） 权值共享（Shared Weights） 在CNN中，卷积层使用滤波器（或卷积核）对输入进行卷积操作。这些滤波器在图像的不同位置都使用相同的参数进行特征提取。这种参数共享机制可以大大减少需要训练的参数数量，因为每个滤波器的参数都被重复使用在输入的不同位置上

3） 池化（Pooling） 池化层通过对输入数据进行下采样，减少了每个特征图的尺寸，从而减少了后续层的计算量。这有助于降低模型的复杂度和计算成本。

来降低参数量

CNN池化的意义

​ CNN池化可以通过池化层来降低卷积层输出的特征维度，在有效减少⽹络参数的同时还可以防⽌过拟合现象。

更大的接受域

image-20240110112037597